This R Statistics book provides a solid step-by-step practical guide to statistical inference for comparing groups means using the R software. Additionally, we developed an R package named rstatix (https://rpkgs.datanovia.com/rstatix/), which provides a simple and intuitive pipe-friendly framework, coherent with the tidyverse design philosophy, for computing the most common statistical analyses, including t-test, Wilcoxon test, ANOVA, Kruskal-Wallis and correlation analyses, outliers identification and more.

This book is designed to get you doing the statistical tests in R as quick as possible. The book focuses on implementation and understanding of the methods, without having to struggle through pages of mathematical proofs.

You will be guided through the steps of summarizing and visualizing the data, checking the assumptions and performing statistical tests in R, interpreting and reporting the results.

Key features of this book

Although there are several good books on statistics and related topics, we felt that many of them are too theoretical. Our goal was to write a practical guide to statistics in R with visualization, interpretation and reporting the results.

The main parts of the book include:

• statistical tests and assumptions for the comparison of groups means,
• comparing two means,
  • t-test,
  • Wilcoxon test,
  • Sign test,
• comparing multiple means,
  • ANOVA - Analysis of Variance for independent measures
  • repeated measures ANOVA,
  • mixed ANOVA,
  • ANCOVA and MANOVA,
  • Kruskal-Wallis test
  • Friedman test

The book presents the basic principles of these tasks and provide many examples in R. This book offers solid guidance in statistics for students and researchers.

Key features:

• Covers the most common statistical tests and implementations
• Key assumptions are presented and checked
• Short, self-contained chapters with practical examples. This means that, you don’t need to read the different chapters in sequence.

How this book is organized ?

This book contains 3 parts. After a quick introduction to R (Chapter @ref(introduction-to-r)), Part I introduces some research questions and the corresponding statistical tests, as well as, the assumptions of the tests. Many of the statistical methods including t-test and analysis of variance (ANOVA) assume some characteristics about the data, including normality of the data distributions and equality of group variances. These assumptions should be taken seriously to draw reliable interpretation and conclusions of the research. In Part I, you will learn how to assess normality using the Shapiro-Wilk test (Chapter @ref(normality-test-in-r)) and how to compare variances in R using Levene’s test and more (Chapter @ref(homogeneity-of-variance)).

Examples of distribution shapes

• Normal distribution

• Skewed distributions

In Part II, we consider how to compare two means using t-test (parametric method, Chapter @ref(t-test)) and wilcoxon test (non-parametric method, Chapter @ref(wilcoxon-test)). Main contents, include:

1. Comparing one-sample mean to a standard known mean:
   • One-Sample T-test (parametric)
   • Wilcoxon Signed Rank Test (non-parametric)
2. Comparing the means of two independent groups:
   • Independent Samples T-test (parametric)
   • Wilcoxon Rank Sum Test (non-parametric)
3. Comparing the means of paired samples:
   • Paired Samples T-test (parametric)
   • Wilcoxon Signed Rank Test on Paired Samples (non-parametric)

In this Part, we also described how to check t-test assumptions, as well as, how to compute the t-test effect size (Cohen’s d). You will also learn how to compute the Wilcoxon effect size. Additionally, we present the sign test (Chapter @ref(sign-test)), an alternative to the paired-samples t-test and the Wilcoxon signed-rank test, in the situation where the distribution of differences between paired data values is neither normal (in t-test) nor symmetrical (in Wilcoxon test).

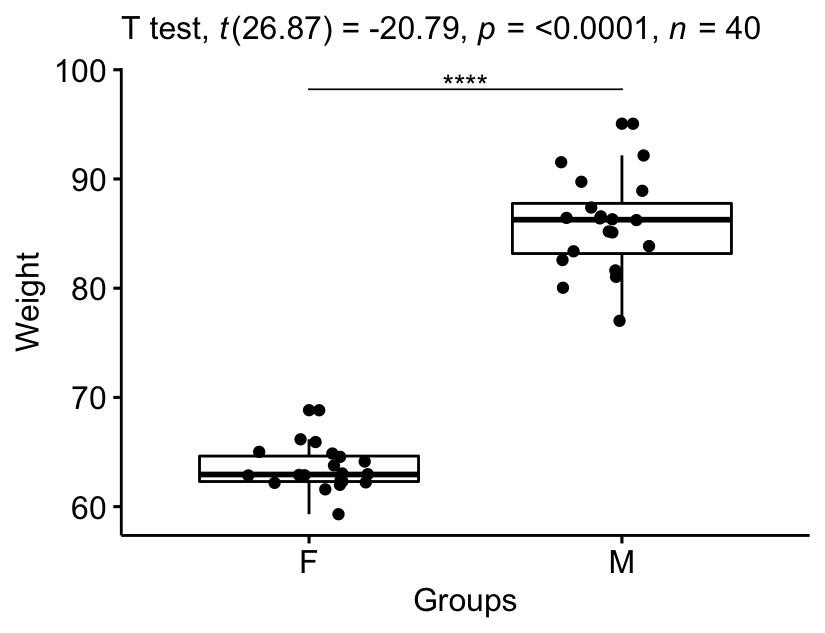
Part III describes how to compare multiple means in R using ANOVA (Analysis of Variance) method and variants (Chapters @ref(anova-analysis-of-variance) - @ref(friedman-test)).

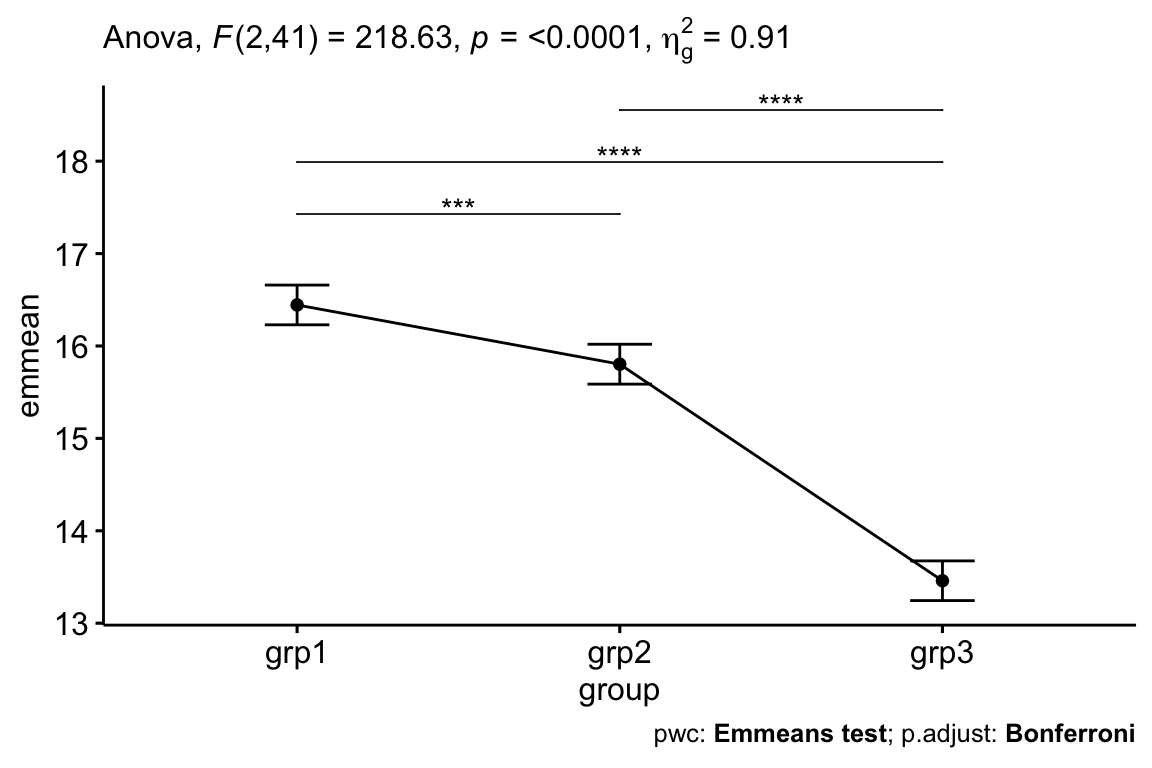
Chapter @ref(anova-analysis-of-variance) describes how to compute and interpret the different types of ANOVA for comparing independent measures, including:

• One-way ANOVA, an extension of the independent samples t-test for comparing the means in a situation where there are more than two groups.
• two-way ANOVA for assessing an interaction effect between two independent categorical variables on a continuous outcome variable.
• three-way ANOVA for assessing an interaction effect between three independent categorical variables on a continuous outcome variable.

We also provide R code to check ANOVA assumptions and perform Post-Hoc analyses. Additionally, we’ll present the Kruskal-Wallis test (Chapter @ref(kruskal-wallis-test-in-r)), which is a non-parametric alternative to the one-way ANOVA test.

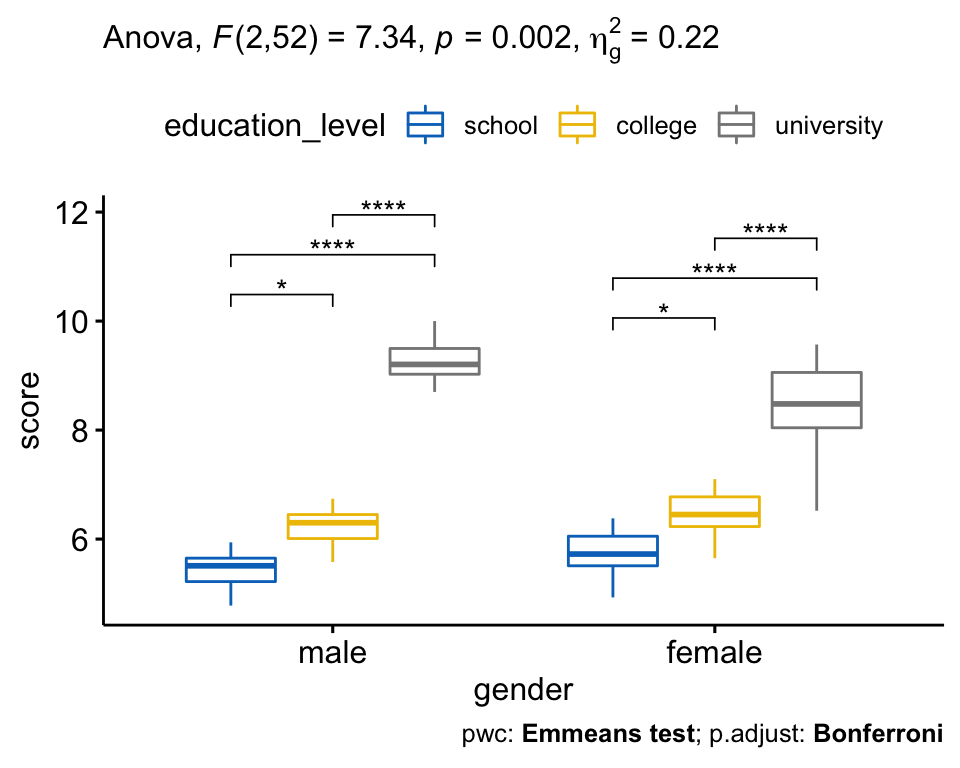
Chapter @ref(repeated-measure-anova) presents repeated-measures ANOVA, which is used for analyzing data where same subjects are measured more than once. You will learn different types of repeated measures ANOVA, including:

• One-way repeated measures ANOVA for comparing the means of three or more levels of a within-subjects variable.
• two-way repeated measures ANOVA used to evaluate simultaneously the effect of two within-subject factors on a continuous outcome variable.
• three-way repeated measures ANOVA used to evaluate simultaneously the effect of three within-subject factors on a continuous outcome variable.

You will also learn how to compute and interpret the Friedman test (Chapter @ref(friedman-test)), which is a non-parametric alternative to the one-way repeated measures ANOVA test.

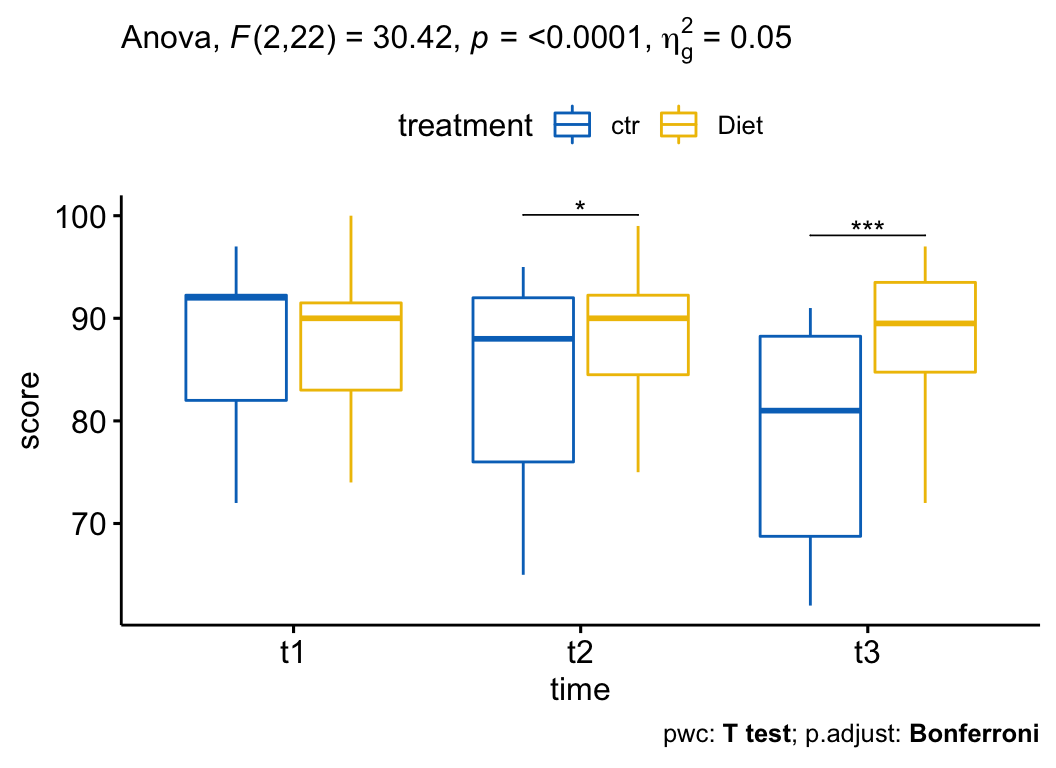
Chapter @ref(mixed-anova) shows how to run mixed ANOVA, which is used to compare the means of groups cross-classified by at least two factors, where one factor is a “within-subjects” factor (repeated measures) and the other factor is a “between-subjects” factor.

Chapters @ref(ancova) and @ref(one-way-manova) describe, respectively, some advanced extensions of ANOVA, including:

• ANCOVA (analyse of covariance), an extension of the one-way ANOVA that incorporate a covariate variable.
• MANOVA (multivariate analysis of variance), an ANOVA with two or more continuous outcome variables.