Advanced Clustering

Required R packages

We’ll use the following R packages: 1) cluster for computing fuzzy clustering and 2) factoextra for visualizing clusters.

Computing fuzzy clustering

The function fanny() [cluster R package] can be used to compute fuzzy clustering. FANNY stands for fuzzy analysis clustering. A simplified format is:

fanny(x, k, metric = "euclidean", stand = FALSE)

The function fanny() returns an object including the following components:

• membership: matrix containing the degree to which each observation belongs to a given cluster. Column names are the clusters and rows are observations
• coeff: Dunn’s partition coefficient F(k) of the clustering, where k is the number of clusters. F(k) is the sum of all squared membership coefficients, divided by the number of observations. Its value is between 1/k and 1. The normalized form of the coefficient is also given. It is defined as \((F(k) - 1/k) / (1 - 1/k)\), and ranges between 0 and 1. A low value of Dunn’s coefficient indicates a very fuzzy clustering, whereas a value close to 1 indicates a near-crisp clustering.
• clustering: the clustering vector containing the nearest crisp grouping of observations

For example, the R code below applies fuzzy clustering on the USArrests data set:

library(cluster)
df <- scale(USArrests)     # Standardize the data
res.fanny <- fanny(df, 2)  # Compute fuzzy clustering with k = 2

The different components can be extracted using the code below:

head(res.fanny$membership, 3) # Membership coefficients

##          [,1]  [,2]
## Alabama 0.664 0.336
## Alaska  0.610 0.390
## Arizona 0.686 0.314

res.fanny$coeff # Dunn's partition coefficient

## dunn_coeff normalized 
##      0.555      0.109

head(res.fanny$clustering) # Observation groups

##    Alabama     Alaska    Arizona   Arkansas California   Colorado 
##          1          1          1          2          1          1

To visualize observation groups, use the function fviz_cluster() [factoextra package]:

library(factoextra)
fviz_cluster(res.fanny, ellipse.type = "norm", repel = TRUE,
             palette = "jco", ggtheme = theme_minimal(),
             legend = "right")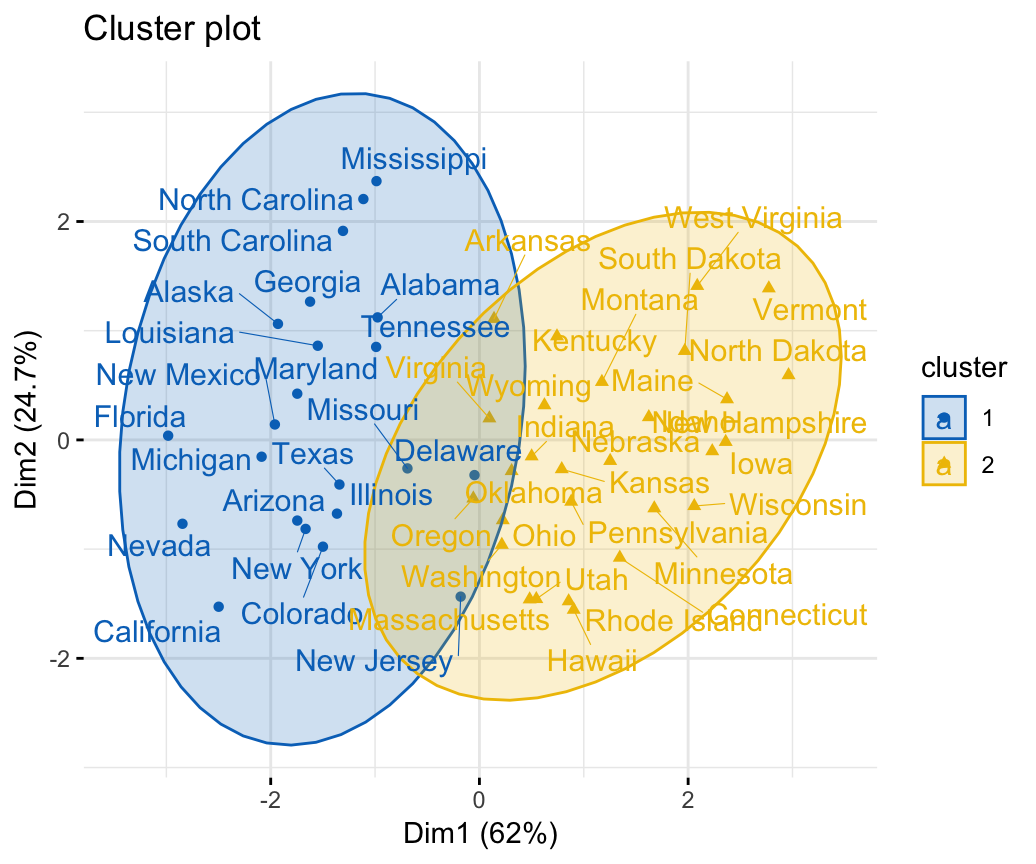

To evaluate the goodnesss of the clustering results, plot the silhouette coefficient as follow:

fviz_silhouette(res.fanny, palette = "jco",
                ggtheme = theme_minimal())

##   cluster size ave.sil.width
## 1       1   22          0.32
## 2       2   28          0.44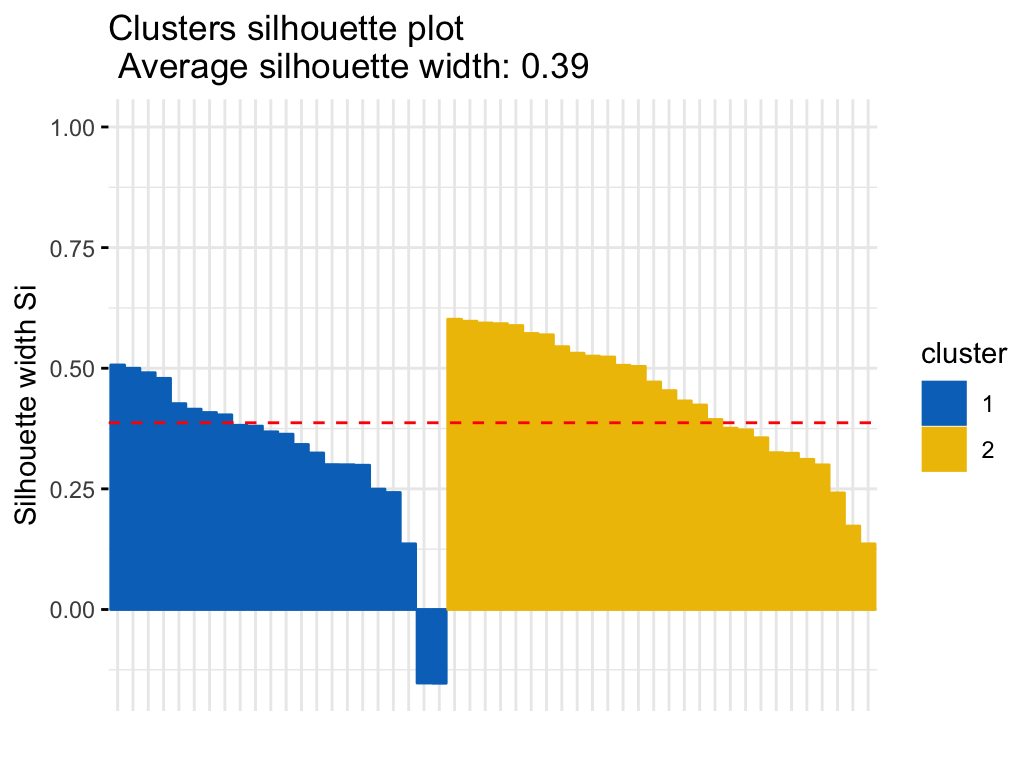

Summary

Fuzzy clustering is an alternative to k-means clustering, where each data point has membership coefficient to each cluster. Here, we demonstrated how to compute and visualize fuzzy clustering using the combination of cluster and factoextra R packages.