Comparing Means of Two Groups in R

Home Comparing Means of Two Groups in R Wilcoxon Test in R

Wilcoxon Test in R

20 mins

Comparing Means of Two Groups in R

109812781077  
78
Shares

The Wilcoxon test is a non-parametric alternative to the t-test for comparing two means. It’s particularly recommended in a situation where the data are not normally distributed.

Like the t-test, the Wilcoxon test comes in two forms, one-sample and two-samples. They are used in more or less the exact same situations as the corresponding t-tests.

Note that, the sample size should be at least 6. Otherwise, the Wilcoxon test cannot become significant.

In this chapter, you will learn how to compute the different types of Wilcoxon tests in R, including:

  • One-sample Wilcoxon signed rank test
  • Wilcoxon rank sum test and
  • Wilcoxon signed rank test on paired samples
  • Check Wilcoxon test assumptions
  • Calculate and report Wilcoxon test effect size (r value).

The effect size r is calculated as Z statistic divided by the square root of the sample size (N) (Z/sqrt(N)). The Z value is extracted from either coin::wilcoxsign_test() (case of one- or paired-samples test) or coin::wilcox_test() (case of independent two-samples test).

Note that N corresponds to the total sample size for independent-samples test and to the total number of pairs for paired samples test. The r value varies from 0 to close to 1. The interpretation values for r commonly in published literature are: 0.10 - < 0.3 (small effect), 0.30 - < 0.5 (moderate effect) and >= 0.5 (large effect).

We’ll use the pipe-friendly function wilcox_test() [rstatix package].



Contents:

Related Book

Practical Statistics in R II - Comparing Groups: Numerical Variables

Prerequisites

Make sure that you have installed the following R packages:

  • tidyverse for data manipulation and visualization
  • ggpubr for creating easily publication ready plots
  • rstatix provides pipe-friendly R functions for easy statistical analyses
  • datarium: contains required datasets for this chapter

Start by loading the following required packages:

library(tidyverse)
library(rstatix)
library(ggpubr)

One-sample Wilcoxon signed rank test

The one-sample Wilcoxon signed rank test is used to assess whether the median of the sample is equal to a known standard or theoretical value. This is a non-parametric equivalent of one-sample t-test.

Demo data

Demo dataset: mice [in datarium package]. Contains the weight of 10 mice:

# Load and inspect the data
data(mice, package = "datarium")
head(mice, 3)
## # A tibble: 3 x 2
##   name  weight
##   <chr>  <dbl>
## 1 M_1     18.9
## 2 M_2     19.5
## 3 M_3     23.1

Summary statistics

Compute the median and the interquartile range (IQR):

mice %>% get_summary_stats(weight, type = "median_iqr")
## # A tibble: 1 x 4
##   variable     n median   iqr
##   <chr>    <dbl>  <dbl> <dbl>
## 1 weight      10   19.8   1.8

Visualization

Create a box plot to visualize the distribution of mice weights. Add also jittered points to show individual observations. The big dot represents the mean point.

bxp <- ggboxplot(
  mice$weight, width = 0.5, add = c("mean", "jitter"), 
  ylab = "Weight (g)", xlab = FALSE
  )
bxp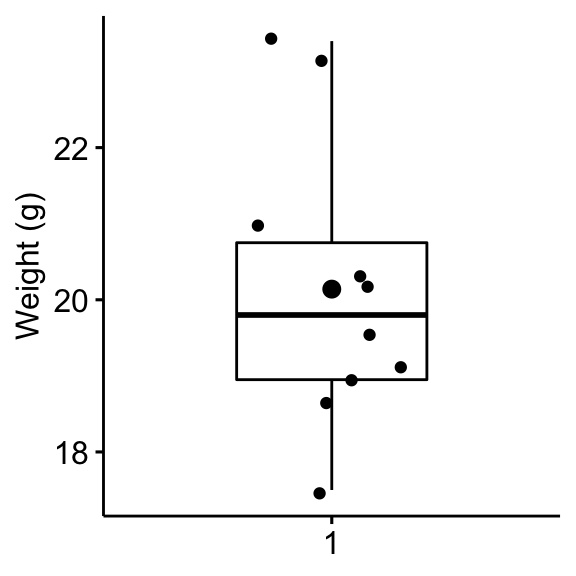

Assumptions and preliminary tests

The Wilcoxon signed-rank test assumes that the data are distributed symmetrically around the median. This can be checked by visual inspection using histogram and density distribution.

Create a histogram: As we have only 10 individuals in our data, we specify the option bins = 4 instead of 30 (default).

gghistogram(mice, x = "weight", y = "..density..", 
            fill = "steelblue",bins = 4, add_density = TRUE)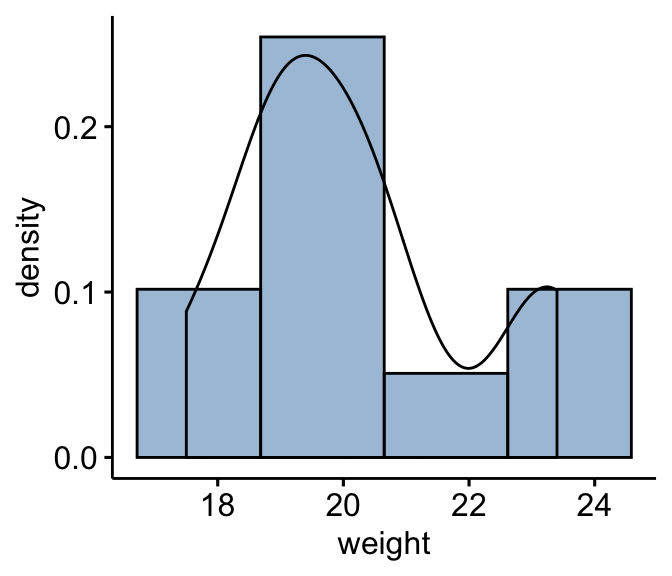

From the plot above, it can be seen that the weight data are approximately symmetrical (you should not expect them to be perfect, particularly when you have smaller numbers of samples in your study). Therefore, we can use the Wilcoxon signed-rank test to analyse our data.

Note that, in the situation where your data is not symmetrically distributed, you could consider performing a sign test, instead of running the Wilcoxon signed-rank test.

The sign test does not make the assumption of a symmetrically-shaped distribution. However, it will most likely be less powerful compared to the Wilcoxon test.

Computation

We want to know, whether the median weight of the mice differs from 25g (two-tailed test)?

stat.test <- mice %>% wilcox_test(weight ~ 1, mu = 25)
stat.test
## # A tibble: 1 x 6
##   .y.    group1 group2         n statistic       p
## * <chr>  <chr>  <chr>      <int>     <dbl>   <dbl>
## 1 weight 1      null model    10         0 0.00195

Note that, to compute one-sided wilcoxon test, you can specify the option alternative, which possible values can be “greater”, “less” or “two.sided”.

Effect size

We’ll use the R function wilcox_effsize() [rstatix]. It requires the coin package for computing the Z statistic.

mice %>%  wilcox_effsize(weight ~ 1, mu = 25)
## # A tibble: 1 x 6
##   .y.    group1 group2     effsize     n magnitude
## * <chr>  <chr>  <chr>        <dbl> <int> <ord>    
## 1 weight 1      null model   0.886    10 large

A large effect size is detected, r = 0.89.

Report

We could report the result as follow:

A Wilcoxon signed-rank test was computed to assess whether the recruited mice median weight was different to the population normal median weight (25g).

The mice weight value were approximately symmetrically distributed, as assessed by a histogram with superimposed density curve.

The measured mice median weight (19.8) was statistically significantly lower than the population median weight 25g (p = 0.002, effect size r = 0.89).

Create a box plot with p-value:

bxp + 
  labs(subtitle = get_test_label(stat.test, detailed = TRUE))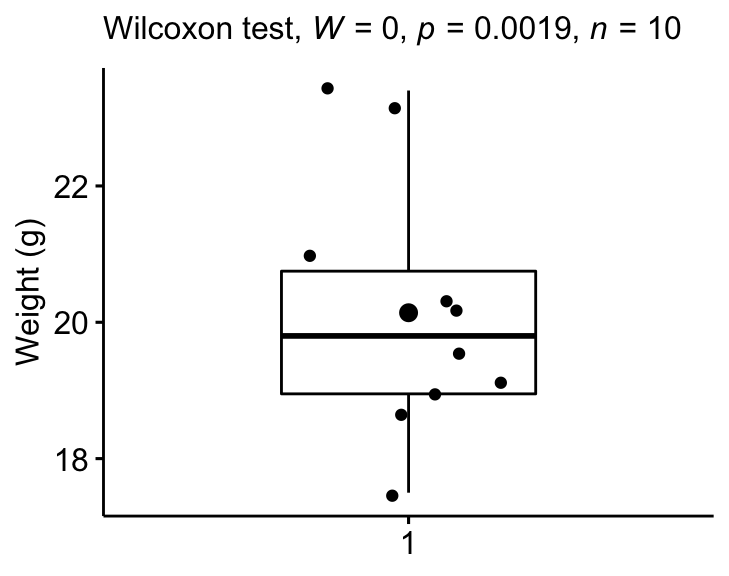

Create a density plot with p-value:

  • Red line corresponds to the observed median
  • Blue line corresponds to the theoretical median
ggdensity(mice, x = "weight", rug = TRUE, fill = "lightgray") +
  scale_x_continuous(limits = c(15, 27)) +
  stat_central_tendency(type = "median", color = "red", linetype = "dashed") +
  geom_vline(xintercept = 25, color = "blue", linetype = "dashed") + 
  labs(subtitle = get_test_label(stat.test, detailed = TRUE))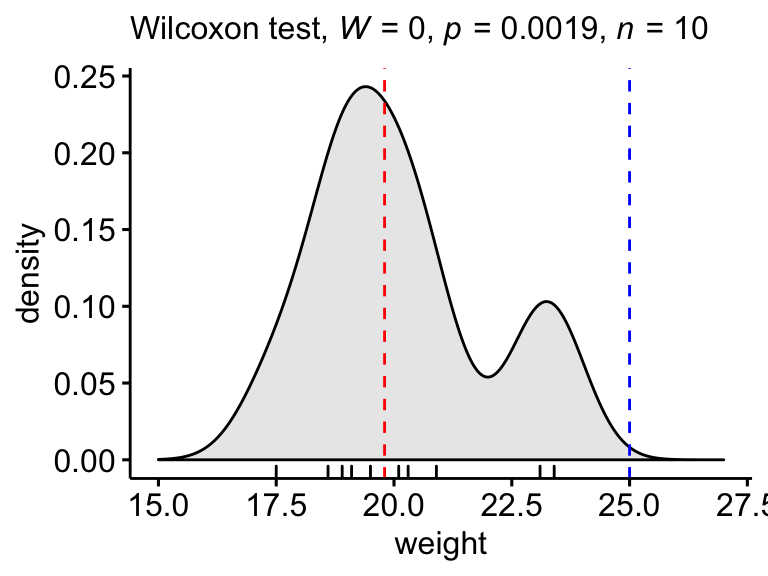

Wilcoxon rank sum test

The Wilcoxon rank sum test is a non-parametric alternative to the independent two samples t-test for comparing two independent groups of samples, in the situation where the data are not normally distributed.

Synonymous: Mann-Whitney test, Mann-Whitney U test, Wilcoxon-Mann-Whitney test and two-sample Wilcoxon test.

Demo data

Demo dataset: genderweight [in datarium package] containing the weight of 40 individuals (20 women and 20 men).

Load the data and show some random rows by groups:

# Load the data
data("genderweight", package = "datarium")
# Show a sample of the data by group
set.seed(123)
genderweight %>% sample_n_by(group, size = 2)
## # A tibble: 4 x 3
##   id    group weight
##   <fct> <fct>  <dbl>
## 1 6     F       65.0
## 2 15    F       65.9
## 3 29    M       88.9
## 4 37    M       77.0

Summary statistics

Compute some summary statistics by groups: median and interquartile range.

genderweight %>%
  group_by(group) %>%
  get_summary_stats(weight, type = "median_iqr")
## # A tibble: 2 x 5
##   group variable     n median   iqr
##   <fct> <chr>    <dbl>  <dbl> <dbl>
## 1 F     weight      20   62.9  2.33
## 2 M     weight      20   86.3  4.59

Visualization

Visualize the data using box plots. Plot weight by groups.

bxp <- ggboxplot(
  genderweight, x = "group", y = "weight", 
  ylab = "Weight", xlab = "Groups", add = "jitter"
  )
bxp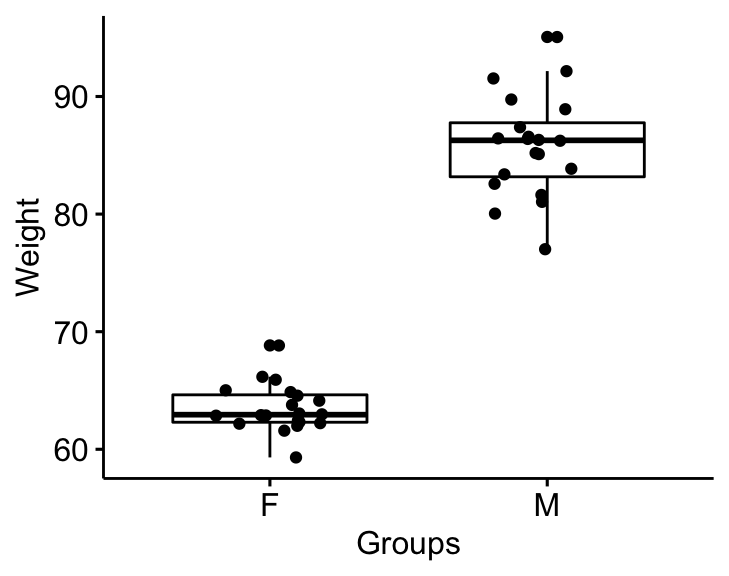

Computation

Question : Is there any significant difference between women and men median weights?

stat.test <- genderweight %>% 
  wilcox_test(weight ~ group) %>%
  add_significance()
stat.test
## # A tibble: 1 x 8
##   .y.    group1 group2    n1    n2 statistic        p p.signif
##   <chr>  <chr>  <chr>  <int> <int>     <dbl>    <dbl> <chr>   
## 1 weight F      M         20    20         0 1.45e-11 ****


Effect size

genderweight %>% wilcox_effsize(weight ~ group)
## # A tibble: 1 x 7
##   .y.    group1 group2 effsize    n1    n2 magnitude
## * <chr>  <chr>  <chr>    <dbl> <int> <int> <ord>    
## 1 weight F      M        0.855    20    20 large

A large effect size is detected, r = 0.86.

Report

We could report the result as follow:

The median weight in female group was 62.9 (IQR = 2.33), whereas the median in male group was 86.3 (IQR = 4.59). The Wilcoxon test showed that the difference was significant (p < 0.0001, effect size r = 0.86).

stat.test <- stat.test %>% add_xy_position(x = "group")
bxp + 
  stat_pvalue_manual(stat.test, tip.length = 0) +
  labs(subtitle = get_test_label(stat.test, detailed = TRUE))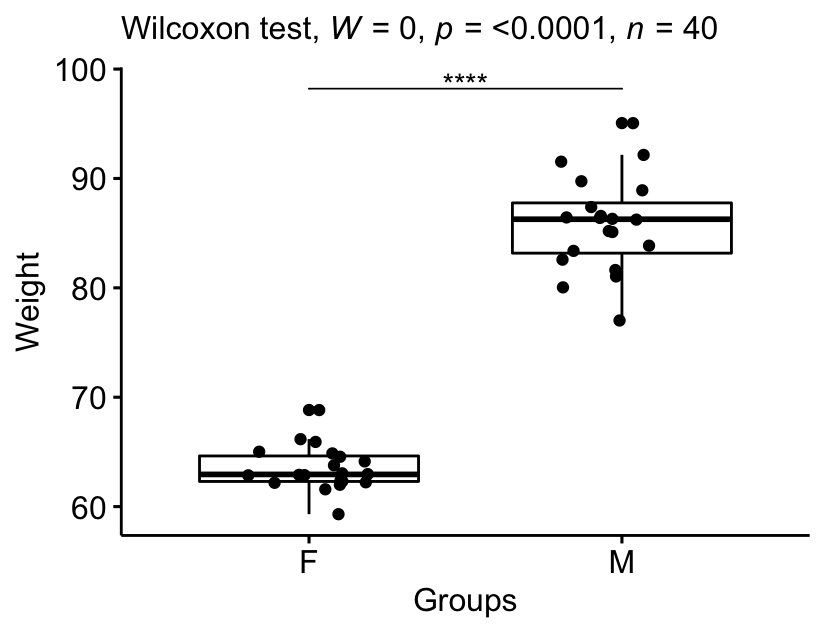

Wilcoxon signed rank test on paired samples

The Wilcoxon signed rank test on paired sample is a non-parametric alternative to the paired samples t-test for comparing paired data. It’s used when the data are not normally distributed.

Demo dataset

Here, we’ll use a demo dataset mice2 [datarium package], which contains the weight of 10 mice before and after the treatment.

# Wide format
data("mice2", package = "datarium")
head(mice2, 3)
##   id before after
## 1  1    187   430
## 2  2    194   404
## 3  3    232   406
# Transform into long data: 
# gather the before and after values in the same column
mice2.long <- mice2 %>%
  gather(key = "group", value = "weight", before, after)
head(mice2.long, 3)
##   id  group weight
## 1  1 before    187
## 2  2 before    194
## 3  3 before    232

Summary statistics

Compute some summary statistics by groups: median and interquartile range (IQR).

mice2.long %>%
  group_by(group) %>%
  get_summary_stats(weight, type = "median_iqr")
## # A tibble: 2 x 5
##   group  variable     n median   iqr
##   <chr>  <chr>    <dbl>  <dbl> <dbl>
## 1 after  weight      10   405   28.3
## 2 before weight      10   197.  19.2

Visualization

bxp <- ggpaired(mice2.long, x = "group", y = "weight", 
         order = c("before", "after"),
         ylab = "Weight", xlab = "Groups")
bxp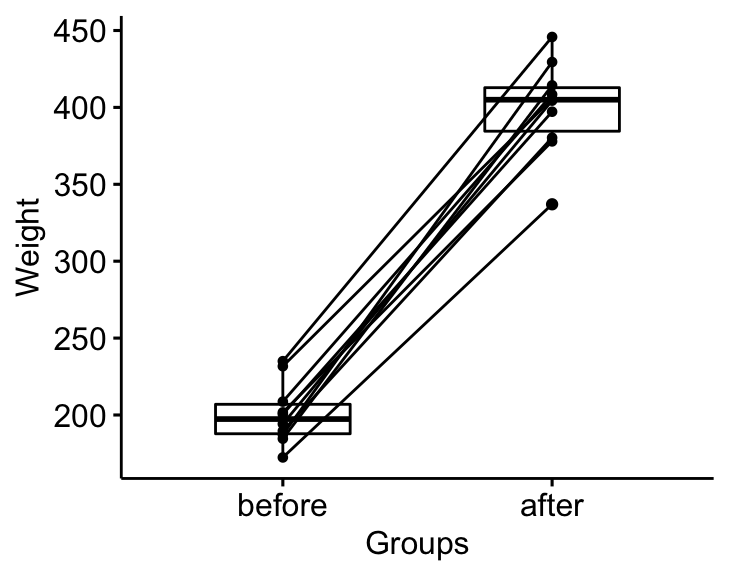

Assumptions and preliminary tests

The test assumes that differences between paired samples should be distributed symmetrically around the median.

Compute the differences between pairs and create histograms:

mice2 <- mice2 %>% mutate(differences = after - before)
gghistogram(mice2, x = "differences", y = "..density..", 
            fill = "steelblue",bins = 5, add_density = TRUE)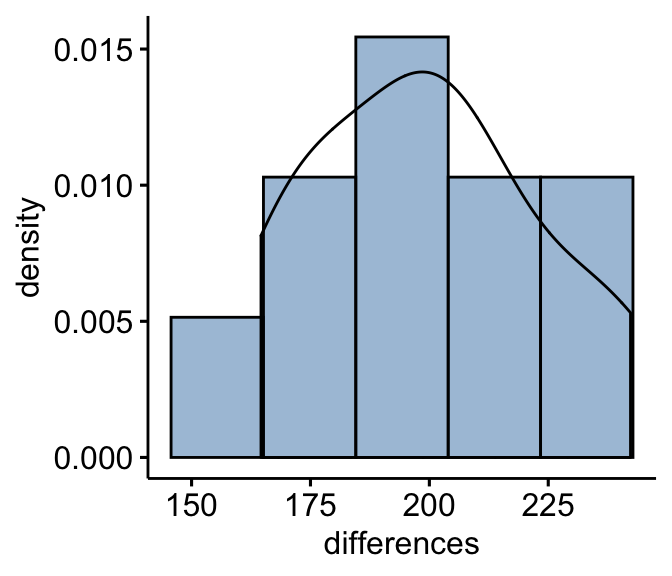

From the plot above, it can be seen that the differences data are approximately symmetrical (you should not expect them to be perfect, particularly when you have smaller numbers of samples in your study). Therefore, we can use the Wilcoxon signed-rank test to analyse our data.

Note that, in the situation where your data is not symmetrically distributed, you could consider performing a sign test, instead of running the Wilcoxon signed-rank test.

The sign test does not make the assumption of a symmetrically-shaped distribution. However, it will most likely be less powerful compared to the Wilcoxon test.

Computation

Question : Is there any significant changes in the weights of mice after treatment?

stat.test <- mice2.long  %>%
  wilcox_test(weight ~ group, paired = TRUE) %>%
  add_significance()
stat.test
## # A tibble: 1 x 8
##   .y.    group1 group2    n1    n2 statistic       p p.signif
##   <chr>  <chr>  <chr>  <int> <int>     <dbl>   <dbl> <chr>   
## 1 weight after  before    10    10        55 0.00195 **

Effect size

mice2.long  %>%
  wilcox_effsize(weight ~ group, paired = TRUE)
## # A tibble: 1 x 7
##   .y.    group1 group2 effsize    n1    n2 magnitude
## * <chr>  <chr>  <chr>    <dbl> <int> <int> <ord>    
## 1 weight after  before   0.886    10    10 large

A large effect size is detected, r = 0.89.

Report

From the output above, it can be concluded that the median weight of the mice before treatment is significantly different from the median weight after treatment with a p-value = 0.002, effect size r = 0.89.

stat.test <- stat.test %>% add_xy_position(x = "group")
bxp + 
  stat_pvalue_manual(stat.test, tip.length = 0) +
  labs(subtitle = get_test_label(stat.test, detailed= TRUE))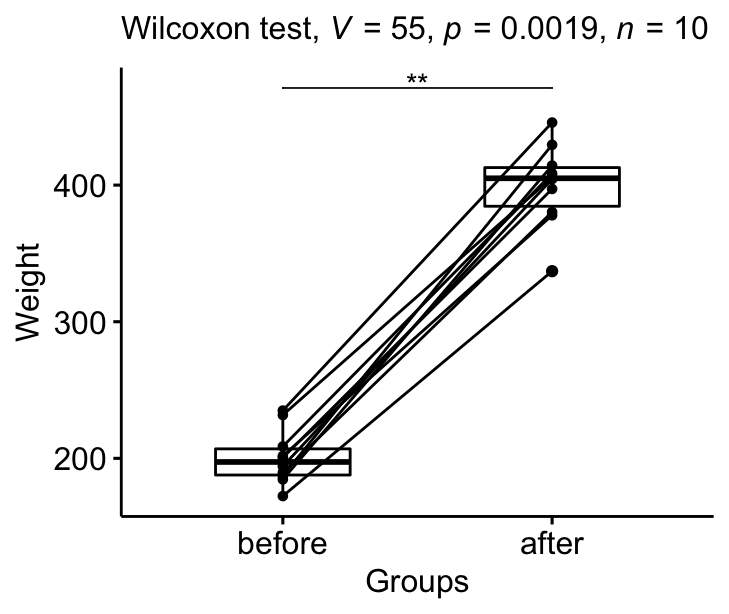

Summary

This chapter describes how to compare two means in R using the Wilcoxon test, which is a non-parametric alternative of the t-test.

Quick start R codes, to compute the different Wilcoxon tests, are:

# One-sample Wilcoxon signed rank test
mice %>% wilcox_test(weight ~ 1, mu = 25)
# Wilcoxon rank sum test: independent samples
genderweight %>% wilcox_test(weight ~ group)
# Wilcoxon signed rank test on paired samples
mice2.long %>% wilcox_test(weight ~ group, paired = TRUE)

Note that, to compute one-sided Wilcoxon tests, you can specify the option alternative, which possible values can be “greater”, “less” or “two.sided”.



 
          

Version: Français

T-test in R (Prev Lesson)
(Next Lesson) Sign Test in R
Back to Comparing Means of Two Groups in R

Comments ( 21 )

  • JooYoung Seo
    29 Dec 2019

    This is amazingly helpful tutorial! I really appreciate it.

    Would you mind if I ask one simple question?

    It says …

    > The Wilcoxon signed-rank test assumes that the data are distributed symmetrically around the median.

    I appreciate the way that you introduced a histogram visualization method to test this assumption; however, would there be any way for non-visual learners (i.e., blind people) to test this assumption using R code instead of the visualization technique? I am asking this because I am blind so it would be more than helpful for me to analyze it using R code.

    Any advice would be so much appreciated.

    Reply
    • Kassambara
      29 Dec 2019

      Thank you for your positive feedback, highly appreciated.

      The function `symmetry.test()` [lawstat packaga] can be used to check whether the data is symmetrically distributed around the median. This function replaces the mean and standard deviation in the classic measure of asymmetry by corresponding robust estimators; the median and mean deviation from the median.

      Statistical hypothesis:
      – Null hypothesis: the data is symmetric
      – Alternative hypothesis: the data is not symmetric

      Example of usage:

      library(lawstat)
mice.weight <- c(18.9, 19.5, 23.1, 20.1, 20.3, 23.4, 20.9, 17.5, 18.6, 19.1)
symmetry.test(mice.weight, boot = FALSE)

      In the example above, the p-value is not significant (p = 0.4), so we accept the null hypothesis: Our data is symmetrically distributed around the median.

      Reply
  • Sfuentes
    17 Apr 2020

    Hi,
    Wonderful tutorial, I’ve been following these also from STHDA.
    I have troubles using the function: stat_pvalue_manual

    Also with the toy data, I get the following error:
    Warning: Ignoring unknown aesthetics: xmin, xmax, annotations, y_position
    Error in f(…) :
    Can only handle data with groups that are plotted on the x-axis

    Boxplot is fine all the way to that function, any tips?
    Thanks!

    Reply
    • Kassambara
      18 Apr 2020

      Hi,

      Please make sure you have the latest version of ggpubr and rstatix

      Reply
  • Jack
    05 May 2020

    Hi!

    Thank you for this tutorial and tutorial about Friedman test; they have been very helpful. Just making a couple of notes:

    1. In addition to significance and magnitude, I find it important to know the direction of the difference. In the example at hand, one can see it very clearly even from the boxplots, but generally this is not working. After all, we are dealing with test based on ranks, not the original continuous data. This is why I have used the original wilcoxon.test function to calculate the pseudomedian.

    2. Citation from this tutorial: “The Wilcoxon signed-rank test assumes that the data are distributed symmetrically around the median. In other words, there should be roughly the same number of values above and below the median.”

    These two phrases are not equivalent. The latter one is always true because of the definition of the median. The first one is what this test truely assumes; if we choose an arbitrary d, the histogram should be about at the same hight in Md – d and Md + d (Md is the median).

    Reply
    • Kassambara
      06 May 2020

      Thank you for such a great comments. Following your comments, the improvements below have been made:

      1. Updating the rstatix::wilcox_test() to report an estimator for the pseudomedian (one-sample case) or for the difference of the location parameters x-y. The column estimate and the confidence intervals are now displayed in the test result when the option detailed = TRUE is specified in the wilcox_test() and pairwise_wilcox_test() functions. You can install the dev version using devtools::install_github("kassambara/rstatix")

      2. Blog post updated, removing the following sentence “In other words, there should be roughly the same number of values above and below the median”.

      library(rstatix)

# Data preparation
data("ToothGrowth")
df <- ToothGrowth

# Wilcoxon test
df %>% wilcox_test(len ~ supp)
      ## # A tibble: 1 x 7
##   .y.   group1 group2    n1    n2 statistic      p
## * <chr> <chr>  <chr>  <int> <int>     <dbl>  <dbl>
## 1 len   OJ     VC        30    30      576. 0.0645
      # Detailed results showing the estimator for the difference in location
df %>% wilcox_test(len ~ supp, detailed = TRUE)
      ## # A tibble: 1 x 12
##   estimate .y.   group1 group2    n1    n2 statistic      p conf.low conf.high method   alternative
## *    <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl>  <dbl>    <dbl>     <dbl> <chr>    <chr>      
## 1     4.00 len   OJ     VC        30    30      576. 0.0645   -0.100      8.50 Wilcoxon two.sided
      Reply
      • Khemlal Nirmalkar
        19 Sep 2020

        Hi Kassambara, please can you also include in the tutorial, how to apply Wilcox test in whole data frame and p.adjusted value. It would be great to see category name/group, p value, q value in columns. I applied pajusted method but i couldn’t see the q value.
        Thanks

        Reply
        • Kassambara
          19 Sep 2020

          Hi, I’m not sure to understand what do you means by “apply wilcox test in whol data frame”? Do you want to apply the test for each variable in the data frame?

          Reply
  • Valeria
    21 May 2020

    Hi!
    Thank you for this tutorial. I found it very useful. I have a question about the effect size. All of the examples above have a large effect size, but I still don’t understand what this means. Can you please get in details what is the impact of the effect size?

    Reply
  • Valerie Martinez
    01 Jul 2020

    I really appreciate this tutorial. However, whenever I try to reproduce the Wilcoxon test, the following appears:

    Error in UseMethod(“wilcox_test”) : no applicable method for ‘wilcox_test’ applied to an object of class “data.frame”

    This occurred with my own data, but I also tried it with the “Toothgrowth” example above and got the same error message.

    Could you please clarify the issue?

    Reply
    • Johanna W
      18 Nov 2020

      I am coming across the same error. Can anyone help with this?

      Reply
      • Jack Sharples
        13 Dec 2020

        I’m getting this error now even though it was working for me this morning. what gives?

        Reply
      • Jack
        14 Dec 2020

        I solved it today. I think there might be other packages in conflict so you can work around it by specifying the rstatix package:

        rstatix::wilcox_test()

        Reply
        • Jan Pecháček
          17 Dec 2020

          Thank you!!!! Now it wokrs

          Reply
          • Lennard Jer
            20 Aug 2021

            Thank you !!
            I wrote following and it works perfectly!
            Wilc_Mean % rstatix::wilcox_test(Mean_HOR ~ Mean_MYG, paired = TRUE)

  • Anne Mari
    02 Dec 2020

    Hello. I tried the Wilcoxon signed rank test on paired samples as described here, and by using GraphPad Prism. I do not get the same result. How does the wilcox_test deal with cases where there has been no change from before to after? And how does it handle zero’s? For exampled that you looked at the relative abundance of some bacteria in 30 people before and after some treatment. But then you have a couple of people that did not change at all, or you have some people that had 0 abundance before and still 0 abundance after. Thanks

    Reply
  • GPC
    05 Jul 2021

    No assumptions check for the standard Wilcoxon one?

    Reply
  • Adrian
    01 Sep 2021

    It’s worth mentioning, that the stochastic equivalence is a general term and isn’t limited only to the shift in location. You may have perfectly equal medians and it will reject H0 if the dispersions vary. That’s why it’s not a test of medians, but rather pseudo medians, which approach medians, as the data get symmetric and have equal dispersion. You mention the pseudomedians, that’s very good! I write it just because many, many people treat the MW(W) test as a test of medians (or median difference), which *approximates* it only in a certain, special and quite rare case. As the famous article says (can be googled in seconds): “Mann-Whitney fails as a test of medians”. Same about the Kruskal-Wallis or Friedman.

    Reply
  • Ruth
    30 Sep 2021

    Hi,
    thank you for this tutorial
    I’m a bit confused since the title and subtitles talk about mean comparison but everywhere else inside the tutorial it seems that these tests are used for median comparison. Could this be fixed or explained?
    Thanks!

    Reply
  • Julie
    07 Nov 2023

    I know that the pairing is done between the first x and y pair, however, we often have long data formats that are not necessarily ordered in a way that this pairing makes sense. Could I include ID in the analysis to ensure the pairings are made correctly without too much manual work on the data frame?

    Many thanks for considering my request.

    Reply

Give a comment

Want to post an issue with R? If yes, please make sure you have read this: How to Include Reproducible R Script Examples in Datanovia Comments

Course Curriculum

Teacher
Alboukadel Kassambara
Role : Founder of Datanovia
Read More