Comparing Means of Two Groups in R

Prerequisites

Make sure that you have installed the following R packages:

• tidyverse for data manipulation and visualization
• ggpubr for creating easily publication ready plots
• rstatix provides pipe-friendly R functions for easy statistical analyses
• datarium: contains required datasets for this chapter

Start by loading the following required packages:

library(tidyverse)
library(rstatix)
library(ggpubr)

Demo dataset

Here, we’ll use a demo dataset mice2 [datarium package], which contains the weight of 10 mice before and after the treatment.

# Wide data
data("mice2", package = "datarium")
head(mice2, 3)

##   id before after
## 1  1    187   430
## 2  2    194   404
## 3  3    232   406

# Transform into long data: 
# gather the before and after values in the same column
mice2.long <- mice2 %>%
  gather(key = "group", value = "weight", before, after)
head(mice2.long, 3)

##   id  group weight
## 1  1 before    187
## 2  2 before    194
## 3  3 before    232

Statistical hypotheses

The paired-samples sign test evaluates whether the median of paired differences is statistically significantly different to 0.

• Null hypotheses, H0: median of the paired differences = 0
• Alternative hypotheses, Ha: median of the paired differences is different to 0

Summary statistics

Compute some summary statistics by groups: median and interquartile range (IQR).

mice2.long %>%
  group_by(group) %>%
  get_summary_stats(weight, type = "median_iqr")

## # A tibble: 2 x 5
##   group  variable     n median   iqr
##   <chr>  <chr>    <dbl>  <dbl> <dbl>
## 1 after  weight      10   405   28.3
## 2 before weight      10   197.  19.2

Visualization

bxp <- ggpaired(mice2.long, x = "group", y = "weight", 
         order = c("before", "after"),
         ylab = "Weight", xlab = "Groups")
bxp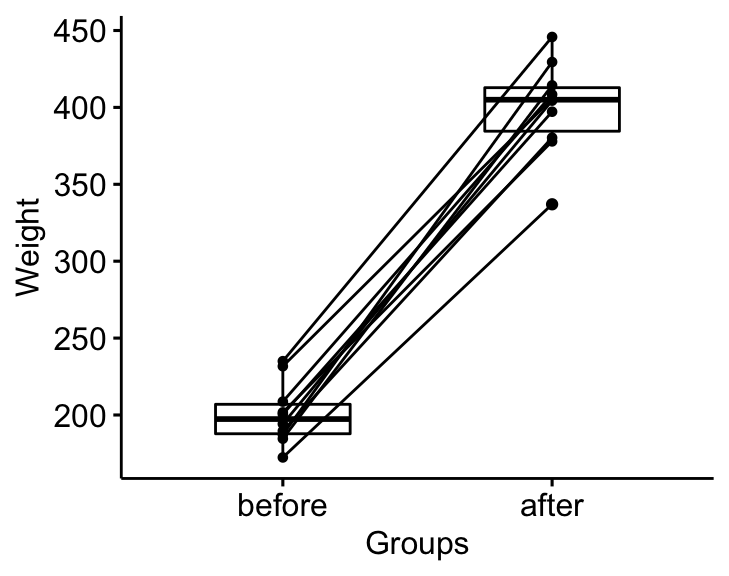

Computation

Question : Is there any significant changes in the weights of mice after treatment?

stat.test <- mice2.long  %>%
  sign_test(weight ~ group) %>%
  add_significance()
stat.test

## # A tibble: 1 x 9
##   .y.    group1 group2    n1    n2 statistic    df       p p.signif
##   <chr>  <chr>  <chr>  <int> <int>     <dbl> <dbl>   <dbl> <chr>   
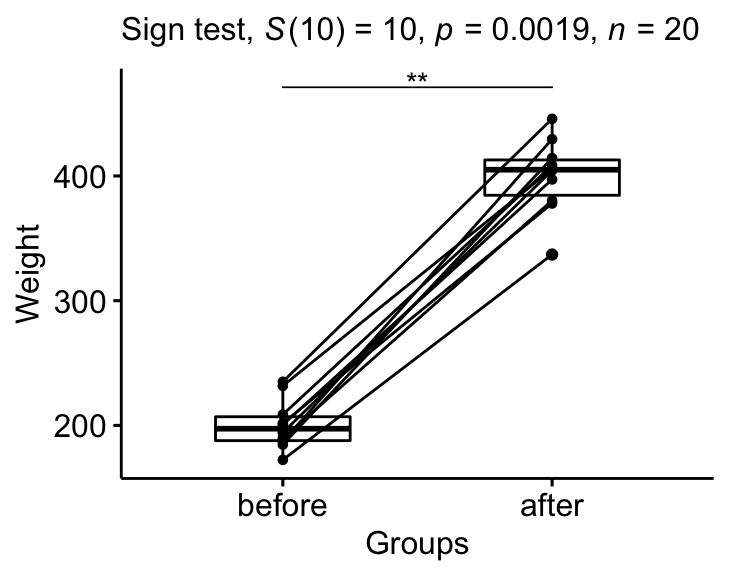
## 1 weight after  before    10    10        10    10 0.00195 **

Report

We could report the results as follow:

The median weight of the mice before treatment is significantly different from the median weight after treatment using sign test, p-value = 0.002.

stat.test <- stat.test %>% add_xy_position(x = "group")
bxp + 
  stat_pvalue_manual(stat.test, tip.length = 0) +
  labs(
  subtitle = get_test_label(stat.test, detailed= TRUE)
  )

Summary

This chapter describes how to compute and report the Sign test in R.