Cohen’s kappa (Jacob Cohen 1960, J Cohen (1968)) is used to measure the agreement of two raters (i.e., “judges”, “observers”) or methods rating on categorical scales. This process of measuring the extent to which two raters assign the same categories or score to the same subject is called inter-rater reliability.
Traditionally, the inter-rater reliability was measured as simple overall percent agreement, calculated as the number of cases where both raters agree divided by the total number of cases considered.
This percent agreement is criticized due to its inability to take into account random or expected agreement by chance, which is the proportion of agreement that you would expect two raters to have based simply on chance.
The Cohen’s kappa is a commonly used measure of agreement that removes this chance agreement. In other words, it accounts for the possibility that raters actually guess on at least some variables due to uncertainty.
There are many situation where you can calculate the Cohen’s Kappa. For example, you might use the Cohen’s kappa to determine the agreement between two doctors in diagnosing patients into “good”, “intermediate” and “bad” prognostic cases.
The Cohen’s kappa can be used for two categorical variables, which can be either two nominal or two ordinal variables. Other variants exists, including:
- Weighted kappa to be used only for ordinal variables.
- Light’s Kappa, which is just the average of all possible two-raters Cohen’s Kappa when having more than two categorical variables (Conger 1980).
- Fleiss kappa, which is an adaptation of Cohen’s kappa for n raters, where n can be 2 or more.
This chapter describes how to measure the inter-rater agreement using the Cohen’s kappa and Light’s Kappa.
You will learn:
- The basics, formula and step-by-step explanation for manual calculation
- Examples of R code to compute Cohen’s kappa for two raters
- How to calculate Light’s kappa for more than two raters
- Interpretation of the kappa coefficient
Contents:
Related Book
Inter-Rater Reliability Essentials: Practical Guide in RBasics and manual calculations
Formula
The formula of Cohen’s Kappa is defined as follow:
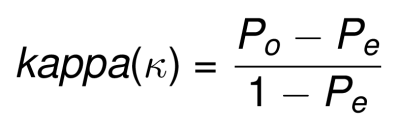
- Po: proportion of observed agreement
- Pe: proportion of chance agreement
kappa can range form -1 (no agreement) to +1 (perfect agreement).
- when k = 0, the agreement is no better than what would be obtained by chance.
- when k is negative, the agreement is less than the agreement expected by chance.
- when k is positive, the rater agreement exceeds chance agreement.
Kappa for 2x2 tables
For explaining how to calculate the observed and expected agreement, let’s consider the following contingency table. Two clinical psychologists were asked to diagnose whether 70 individuals are in depression or not.
Data structure:
## Doctor2
## Doctor1 Yes No Total
## Yes a b R1
## No c d R2
## Total C1 C2 NWhere:
- a, b, c and d are the observed (O) counts of individuals;
- N = a + b + c + d, that is the total table counts;
- R1 and R2 are the total of row 1 and 2, respectively. These represent row margins in the statistics jargon.
- C1 and C2 are the total of column 1 and 2, respectively. These are column margins.
Example of data:
## doctor2
## doctor1 yes no Sum
## yes 25 10 35
## no 15 20 35
## Sum 40 30 70Proportion of observed agreement. The total observed agreement counts is the sum of the diagonal entries. The proportion of observed agreement is: sum(diagonal.values)/N, where N is the total table counts.
- 25 participants were diagnosed yes by the two doctors
- 20 participants were diagnosed no by both
so, Po = (a + d)/N = (25 + 20)/70 = 0.643
Proportion of chance agreement. The expected proportion of agreement is calculated as follow.
Step 1. Determine the probability that both doctors would randomly say Yes:
-
- Doctor 1 says yes to 35/70 (0.5) participants. This represents the row 1 marginal proportion, which is
row1.sum/N.
- Doctor 2 says yes to 40/70 (0.57) participants. This represents the column 1 marginal proportion, which is
column1.sum/N.
- Total probability of both doctors saying yes randomly is
0.5*0.57 = 0.285. This is the product of row 1 and column 1 marginal proportions.
- Doctor 1 says yes to 35/70 (0.5) participants. This represents the row 1 marginal proportion, which is
Step 2. Determine the probability that both doctors would randomly say No:
-
- Doctor 1 says no to 35/70 (0.5) participants. This is the row 2 marginal proportion:
row2.sum/N.
- Doctor 2 says no to 30/70 (0.428) participants. This is the column 2 marginal proportion:
column2.sum/N.
- Total probability of both doctors saying no randomly is
0.5*0.428 = 0.214. This is the product of row 2 and column 2 marginal proportions.
- Doctor 1 says no to 35/70 (0.5) participants. This is the row 2 marginal proportion:
so, the total expected probability by chance is Pe = 0.285+0.214 = 0.499. Technically, this can be seen as the sum of the product of rows and columns marginal proportions: Pe = sum(rows.marginal.proportions x columns.marginal.proportions).
Cohen’s kappa. Finally, the Cohen’s kappa is (0.643 - 0.499)/(1-0.499) = 0.28.
Kappa for two categorical variables with multiple levels
In the previous section, we demonstrated how to manually compute the kappa value for 2x2 table (binomial variables: yes vs no). This can be generalized to categorical variables with multiple levels as follow.
The ratings scores from the two raters can be summarized in a k×k contingency table, where k is the number of categories.
Example of kxk contingency table to assess agreement about k categories by two different raters:
## rater2
## rater1 Level.1 Level.2 Level... Level.k Total
## Level.1 n11 n12 ... n1k n1+
## Level.2 n21 n22 ... n2k n2+
## Level... ... ... ... ... ...
## Level.k nk1 nk2 ... nkk nk+
## Total n+1 n+2 ... n+k NTerminologies:
- The column “Total” (
n1+, n2+, ..., nk+) indicates the sum of each row, known as row margins or marginal counts. Here, the total sum of a given rowiis namedni+. - The row “Total” (
n+1, n+2, ..., n+k) indicates the sum of each column, known as column margins. Here, the total sum of a given columniis namedn+i - N is the total sum of all table cells
- For a give row/column, the marginal proportion is the row/column margin divide by N. This is also known as the marginal frequencies or probabilities. For a row
i, the marginal proportion isPi+ = ni+/N. Similarly, for a given columni, the marginal proportion isP+i = n+i/N. - For each table cell, the proportion can be calculated as the cell count divided by N.
The proportion of observed agreement (Po) is the sum of diagonal proportions, which corresponds to the proportion of cases in each category for which the two raters agreed on the assignment.
The proportion of chance agreement (Pe) is the sum of the products of the rows and columns marginal proportions:pe = sum(row.marginal.proportions x column.marginal.proportions)
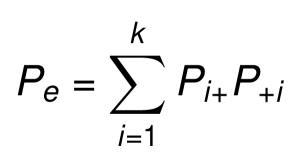
So, the Cohen’s kappa can be calculated by plugging Po and Pe in the formula: k = (Po - Pe)/(1 - Pe).
Kappa confidence intervals. For large sample size, the standard error (SE) of kappa can be computed as follow (J. L. Fleiss and Cohen 1973, J. L. Fleiss, Cohen, and Everitt (1969), Friendly, Meyer, and Zeileis (2015)):
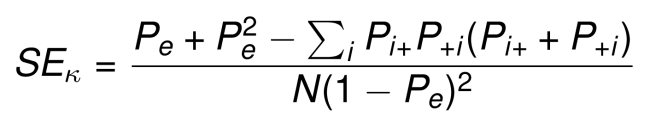
Once SE(k) is calculated, a 100(1 – alpha)% confidence interval for kappa may be computed using the standard normal distribution as follows:
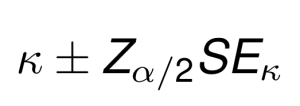
For example, the formula of the 95% confidence interval is: k +/- 1.96 x SE.
R code to compute step by step the Cohen’s kappa:
# Contingency table
xtab <- as.table(rbind(c(25, 10), c(15, 20)))
# Descriptive statistics
diagonal.counts <- diag(xtab)
N <- sum(xtab)
row.marginal.props <- rowSums(xtab)/N
col.marginal.props <- colSums(xtab)/N
# Compute kappa (k)
Po <- sum(diagonal.counts)/N
Pe <- sum(row.marginal.props*col.marginal.props)
k <- (Po - Pe)/(1 - Pe)
kIn the following sections, you will learn a single line R function to compute Kappa.
Interpretation: Magnitude of the agreement
In most applications, there is usually more interest in the magnitude of kappa than in the statistical significance of kappa. The following classifications has been suggested to interpret the strength of the agreement based on the Cohen’s Kappa value (Altman 1999, Landis JR (1977)).
| Value of k | Strength of agreement |
|---|---|
| < 0 | Poor |
| 0.01 - 0.20 | Slight |
| 0.21-0.40 | Fair |
| 0.41-0.60 | Moderate |
| 0.61-0.80 | Substantial |
| 0.81 - 1.00 | Almost perfect |
However, this interpretation allows for very little agreement among raters to be described as “substantial”. According to the table 61% agreement is considered as good, but this can immediately be seen as problematic depending on the field. Almost 40% of the data in the dataset represent faulty data. In healthcare research, this could lead to recommendations for changing practice based on faulty evidence. For a clinical laboratory, having 40% of the sample evaluations being wrong would be an extremely serious quality problem (McHugh 2012).
This is the reason that many texts recommend 80% agreement as the minimum acceptable inter-rater agreement. Any kappa below 0.60 indicates inadequate agreement among the raters and little confidence should be placed in the study results.
Fleiss et al. (2003) stated that for most purposes,
- values greater than 0.75 or so may be taken to represent excellent agreement beyond chance,
- values below 0.40 or so may be taken to represent poor agreement beyond chance, and
- values between 0.40 and 0.75 may be taken to represent fair to good agreement beyond chance.
Another logical interpretation of kappa from (McHugh 2012) is suggested in the table below:
| Value of k | Level of agreement | % of data that are reliable |
|---|---|---|
| 0 - 0.20 | None | 0 - 4‰ |
| 0.21 - 0.39 | Minimal | 4 - 15% |
| 0.40 - 0.59 | Weak | 15 - 35% |
| 0.60 - 0.79 | Moderate | 35 - 63% |
| 0.80 - 0.90 | Strong | 64 - 81% |
| Above 0.90 | Almost Perfect | 82 - 100% |
In the table above, the column “% of data that are reliable” corresponds to the squared kappa, an equivalent of the squared correlation coefficient, which is directly interpretable.
Assumptions and requirements
Your data should met the following assumptions for computing Cohen’s Kappa.
- You have two outcome categorical variables, which can be ordinal or nominal variables.
- The two outcome variables should have exactly the same categories
- You have paired observations; each subject is categorized twice by two independent raters or methods.
- The same two raters are used for all participants.
Statistical hypotheses
- Null hypothesis (H0):
kappa = 0. The agreement is the same as chance agreement. - Alternative hypothesis (Ha):
kappa ≠ 0. The agreement is different from chance agreement.
Example of data
We’ll use the psychiatric diagnoses data provided by two clinical doctors. 30 patients were enrolled and classified by each of the two doctors into 5 categories (J. Fleiss and others 1971): 1. Depression, 2. Personality Disorder, 3. Schizophrenia, 4. Neurosis, 5. Other.
The data is organized into the following 5x5 contingency table:
# Demo data
diagnoses <- as.table(rbind(
c(7, 1, 2, 3, 0), c(0, 8, 1, 1, 0),
c(0, 0, 2, 0, 0), c(0, 0, 0, 1, 0),
c(0, 0, 0, 0, 4)
))
categories <- c("Depression", "Personality Disorder",
"Schizophrenia", "Neurosis", "Other")
dimnames(diagnoses) <- list(Doctor1 = categories, Doctor2 = categories)
diagnoses## Doctor2
## Doctor1 Depression Personality Disorder Schizophrenia Neurosis Other
## Depression 7 1 2 3 0
## Personality Disorder 0 8 1 1 0
## Schizophrenia 0 0 2 0 0
## Neurosis 0 0 0 1 0
## Other 0 0 0 0 4Computing Kappa
Kappa for two raters
The R function Kappa() [vcd package] can be used to compute unweighted and weighted Kappa. The unweighted version corresponds to the Cohen’s Kappa, which are our concern in this chapter. The weighted Kappa should be considered only for ordinal variables and are largely described in Chapter @ref(weighted-kappa).
# install.packages("vcd")
library("vcd")
# Compute kapa
res.k <- Kappa(diagnoses)
res.k## value ASE z Pr(>|z|)
## Unweighted 0.651 0.0997 6.53 6.47e-11
## Weighted 0.633 0.1194 5.30 1.14e-07# Confidence intervals
confint(res.k)##
## Kappa lwr upr
## Unweighted 0.456 0.847
## Weighted 0.399 0.867Note that, in the above results ASE is the asymptotic standard error of the kappa value.
In our example, the Cohen’s kappa (k) = 0.65, which represents a fair to good strength of agreement according to Fleiss e al. (2003) classification. This is confirmed by the obtained p-value (p < 0.05), indicating that our calculated kappa is significantly different from zero.
Kappa for more than two raters
If there are more than 2 raters, then the average of all possible two-raters kappa is known as Light’s kappa (Conger 1980). You can compute it using the function kappam.light() [irr package], which takes a matrix as input. The matrix columns are raters and rows are individuals.
# install.packages("irr")
library(irr)
# Load and inspect a demo data
data("diagnoses", package = "irr")
head(diagnoses[, 1:3], 4)## Doctor2
## Doctor1 Depression Personality Disorder Schizophrenia
## Depression 7 1 2
## Personality Disorder 0 8 1
## Schizophrenia 0 0 2
## Neurosis 0 0 0# Compute Light's kappa between the first 3 raters
kappam.light(diagnoses[, 1:3])## Light's Kappa for m Raters
##
## Subjects = 5
## Raters = 3
## Kappa = 0.172
##
## z = 0.69
## p-value = 0.49Report
Cohen’s kappa was computed to assess the agreement between two doctors in diagnosing the psychiatric disorders in 30 patients. There was a good agreement between the two doctors, kappa = 0.65 (95% CI, 0.46 to 0.84), p < 0.0001.
Summary
This chapter describes the basics and the formula of the Cohen’s kappa. Additionally, we show how to compute and interpret the kappa coefficient in R. We also provide examples of R code for computing the Light’s Kappa, which is the average of all possible two-raters kappa when you have more than two raters.
Other variants of Cohen’s kappa include: the weighted kappa (for two ordinal variables, Chapter @ref(weighted-kappa)) and Fleiss kappa (for two or more variables, Chapter @ref(weighted-kappa)).
References
Altman, Douglas G. 1999. Practical Statistics for Medical Research. Chapman; Hall/CRC Press.
Cohen, J. 1968. “Weighted Kappa: Nominal Scale Agreement with Provision for Scaled Disagreement or Partial Credit.” Psychological Bulletin 70 (4): 213—220. doi:10.1037/h0026256.
Cohen, Jacob. 1960. “A Coefficient of Agreement for Nominal Scales.” Educational and Psychological Measurement 20 (1): 37–46. doi:10.1177/001316446002000104.
Conger, A. J. 1980. “Integration and Generalization of Kappas for Multiple Raters.” Psychological Bulletin 88 (2): 322–28.
Fleiss, J.L., and others. 1971. “Measuring Nominal Scale Agreement Among Many Raters.” Psychological Bulletin 76 (5): 378–82.
Fleiss, Joseph L., and Jacob Cohen. 1973. “The Equivalence of Weighted Kappa and the Intraclass Correlation Coefficient as Measures of Reliability.” Educational and Psychological Measurement 33 (3): 613–19. doi:10.1177/001316447303300309.
Fleiss, Joseph L., Jacob Willem Cohen, and Brian Everitt. 1969. “Large Sample Standard Errors of Kappa and Weighted Kappa.” Psychological Bulletin 72: 332–27.
Friendly, Michael, D. Meyer, and A. Zeileis. 2015. Discrete Data Analysis with R: Visualization and Modeling Techniques for Categorical and Count Data. 1st ed. Chapman; Hall/CRC.
Landis JR, Koch GG. 1977. “The Measurement of Observer Agreement for Categorical Data” 1 (33). Biometrics: 159–74.
McHugh, Mary. 2012. “Interrater Reliability: The Kappa Statistic.” Biochemia Medica : Časopis Hrvatskoga Društva Medicinskih Biokemičara / HDMB 22 (October): 276–82. doi:10.11613/BM.2012.031.
Recommended for you
This section contains best data science and self-development resources to help you on your path.
Coursera - Online Courses and Specialization
Data science
- Course: Machine Learning: Master the Fundamentals by Stanford
- Specialization: Data Science by Johns Hopkins University
- Specialization: Python for Everybody by University of Michigan
- Courses: Build Skills for a Top Job in any Industry by Coursera
- Specialization: Master Machine Learning Fundamentals by University of Washington
- Specialization: Statistics with R by Duke University
- Specialization: Software Development in R by Johns Hopkins University
- Specialization: Genomic Data Science by Johns Hopkins University
Popular Courses Launched in 2020
- Google IT Automation with Python by Google
- AI for Medicine by deeplearning.ai
- Epidemiology in Public Health Practice by Johns Hopkins University
- AWS Fundamentals by Amazon Web Services
Trending Courses
- The Science of Well-Being by Yale University
- Google IT Support Professional by Google
- Python for Everybody by University of Michigan
- IBM Data Science Professional Certificate by IBM
- Business Foundations by University of Pennsylvania
- Introduction to Psychology by Yale University
- Excel Skills for Business by Macquarie University
- Psychological First Aid by Johns Hopkins University
- Graphic Design by Cal Arts
Amazon FBA
Amazing Selling Machine
Books - Data Science
Our Books
- Practical Guide to Cluster Analysis in R by A. Kassambara (Datanovia)
- Practical Guide To Principal Component Methods in R by A. Kassambara (Datanovia)
- Machine Learning Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R Graphics Essentials for Great Data Visualization by A. Kassambara (Datanovia)
- GGPlot2 Essentials for Great Data Visualization in R by A. Kassambara (Datanovia)
- Network Analysis and Visualization in R by A. Kassambara (Datanovia)
- Practical Statistics in R for Comparing Groups: Numerical Variables by A. Kassambara (Datanovia)
- Inter-Rater Reliability Essentials: Practical Guide in R by A. Kassambara (Datanovia)
Others
- R for Data Science: Import, Tidy, Transform, Visualize, and Model Data by Hadley Wickham & Garrett Grolemund
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurelien Géron
- Practical Statistics for Data Scientists: 50 Essential Concepts by Peter Bruce & Andrew Bruce
- Hands-On Programming with R: Write Your Own Functions And Simulations by Garrett Grolemund & Hadley Wickham
- An Introduction to Statistical Learning: with Applications in R by Gareth James et al.
- Deep Learning with R by François Chollet & J.J. Allaire
- Deep Learning with Python by François Chollet
Version:
Français
Is there a square root missing for the Standard Error?