ANCOVA in R: The Ultimate Practical Guide

ANCOVA in R

25 mins

The Analysis of Covariance (ANCOVA) is used to compare means of an outcome variable between two or more groups taking into account (or to correct for) variability of other variables, called covariates. In other words, ANCOVA allows to compare the adjusted means of two or more independent groups.

For example, you might want to compare “test score” by “level of education” taking into account the “number of hours spent studying”. In this example: 1) test score is our outcome (dependent) variable; 2) level of education (high school, college degree or graduate degree) is our grouping variable; 3) sudying time is our covariate.

The one-way ANCOVA can be seen as an extension of the one-way ANOVA that incorporate a covariate variable. The two-way ANCOVA is used to evaluate simultaneously the effect of two independent grouping variables (A and B) on an outcome variable, after adjusting for one or more continuous variables, called covariates.

In this article, you will learn how to:

Compute and interpret the one-way and the two-way ANCOVA in R
Check ANCOVA assumptions
Perform post-hoc tests, multiple pairwise comparisons between groups to identify which groups are different
Visualize the data using box plots, add ANCOVA and pairwise comparisons p-values to the plot

Contents:

Assumptions
Prerequisites
One-way ANCOVA
Two-way ANCOVA
Summary

Related Book

Practical Statistics in R II - Comparing Groups: Numerical Variables

Assumptions

ANCOVA makes several assumptions about the data, such as:

Linearity between the covariate and the outcome variable at each level of the grouping variable. This can be checked by creating a grouped scatter plot of the covariate and the outcome variable.
Homogeneity of regression slopes. The slopes of the regression lines, formed by the covariate and the outcome variable, should be the same for each group. This assumption evaluates that there is no interaction between the outcome and the covariate. The plotted regression lines by groups should be parallel.
The outcome variable should be approximately normally distributed. This can be checked using the Shapiro-Wilk test of normality on the model residuals.
Homoscedasticity or homogeneity of residuals variance for all groups. The residuals are assumed to have a constant variance (homoscedasticity)
No significant outliers in the groups

Many of these assumptions and potential problems can be checked by analyzing the residual errors. In the situation, where the ANCOVA assumption is not met you can perform robust ANCOVA test using the WRS2 package.

Prerequisites

Make sure you have installed the following R packages:

tidyverse for data manipulation and visualization
ggpubr for creating easily publication ready plots
rstatix for easy pipe-friendly statistical analyses
broom for printing a nice summary of statistical tests as data frames
datarium: contains required data sets for this chapter

Start by loading the following required packages:

library(tidyverse)
library(ggpubr)
library(rstatix)
library(broom)

One-way ANCOVA

Data preparation

We’ll prepare our demo data from the anxiety dataset available in the datarium package.

Researchers investigated the effect of exercises in reducing the level of anxiety. Therefore, they conducted an experiment, where they measured the anxiety score of three groups of individuals practicing physical exercises at different levels (grp1: low, grp2: moderate and grp3: high).

The anxiety score was measured pre- and 6-months post-exercise training programs. It is expected that any reduction in the anxiety by the exercises programs would also depend on the participant’s basal level of anxiety score.

In this analysis we use the pretest anxiety score as the covariate and are interested in possible differences between group with respect to the post-test anxiety scores.

# Load and prepare the data
data("anxiety", package = "datarium")
anxiety <- anxiety %>%
  select(id, group, t1, t3) %>%
  rename(pretest = t1, posttest = t3)
anxiety[14, "posttest"] <- 19
# Inspect the data by showing one random row by groups
set.seed(123)
anxiety %>% sample_n_by(group, size = 1)

## # A tibble: 3 x 4
##   id    group pretest posttest
##   <fct> <fct>   <dbl>    <dbl>
## 1 5     grp1     16.5     15.7
## 2 27    grp2     17.8     16.9
## 3 37    grp3     17.1     14.3

Check assumptions

Linearity assumption

Create a scatter plot between the covariate (i.e., pretest) and the outcome variable (i.e., posttest)
Add regression lines, show the corresponding equations and the R2 by groups

ggscatter(
  anxiety, x = "pretest", y = "posttest",
  color = "group", add = "reg.line"
  )+
  stat_regline_equation(
    aes(label =  paste(..eq.label.., ..rr.label.., sep = "~~~~"), color = group)
    )

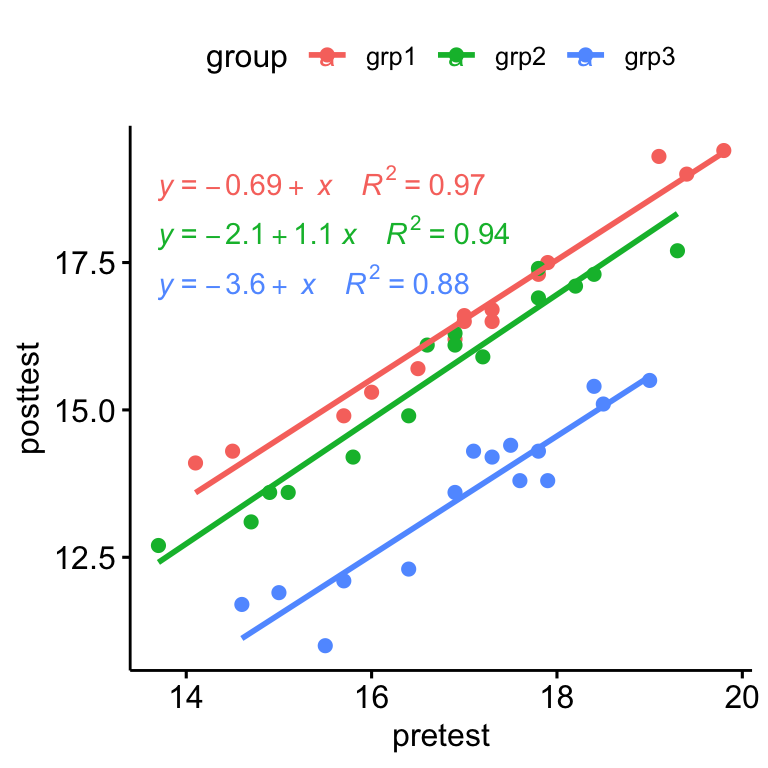
There was a linear relationship between pre-test and post-test anxiety score for each training group, as assessed by visual inspection of a scatter plot.

Homogeneity of regression slopes

This assumption checks that there is no significant interaction between the covariate and the grouping variable. This can be evaluated as follow:

anxiety %>% anova_test(posttest ~ group*pretest)

## ANOVA Table (type II tests)
## 
##          Effect DFn DFd       F        p p<.05   ges
## 1         group   2  39 209.314 1.40e-21     * 0.915
## 2       pretest   1  39 572.828 6.36e-25     * 0.936
## 3 group:pretest   2  39   0.127 8.81e-01       0.006

There was homogeneity of regression slopes as the interaction term was not statistically significant, F(2, 39) = 0.13, p = 0.88.

Normality of residuals

You first need to compute the model using lm(). In R, you can easily augment your data to add fitted values and residuals by using the function augment(model) [broom package]. Let’s call the output model.metrics because it contains several metrics useful for regression diagnostics.

# Fit the model, the covariate goes first
model <- lm(posttest ~ pretest + group, data = anxiety)
# Inspect the model diagnostic metrics
model.metrics <- augment(model) %>%
  select(-.hat, -.sigma, -.fitted, -.se.fit) # Remove details
head(model.metrics, 3)

## # A tibble: 3 x 6
##   posttest pretest group .resid .cooksd .std.resid
##      <dbl>   <dbl> <fct>  <dbl>   <dbl>      <dbl>
## 1     14.1    14.1 grp1   0.550  0.101       1.46 
## 2     14.3    14.5 grp1   0.338  0.0310      0.885
## 3     14.9    15.7 grp1  -0.295  0.0133     -0.750

# Assess normality of residuals using shapiro wilk test
shapiro_test(model.metrics$.resid)

## # A tibble: 1 x 3
##   variable             statistic p.value
##   <chr>                    <dbl>   <dbl>
## 1 model.metrics$.resid     0.975   0.444

The Shapiro Wilk test was not significant (p > 0.05), so we can assume normality of residuals

Homogeneity of variances

ANCOVA assumes that the variance of the residuals is equal for all groups. This can be checked using the Levene’s test:

model.metrics %>% levene_test(.resid ~ group)

## # A tibble: 1 x 4
##     df1   df2 statistic     p
##   <int> <int>     <dbl> <dbl>
## 1     2    42      2.27 0.116

The Levene’s test was not significant (p > 0.05), so we can assume homogeneity of the residual variances for all groups.

Outliers

An outlier is a point that has an extreme outcome variable value. The presence of outliers may affect the interpretation of the model.

Outliers can be identified by examining the standardized residual (or studentized residual), which is the residual divided by its estimated standard error. Standardized residuals can be interpreted as the number of standard errors away from the regression line.

Observations whose standardized residuals are greater than 3 in absolute value are possible outliers.

model.metrics %>% 
  filter(abs(.std.resid) > 3) %>%
  as.data.frame()

## [1] posttest   pretest    group      .resid     .cooksd    .std.resid
## <0 rows> (or 0-length row.names)

There were no outliers in the data, as assessed by no cases with standardized residuals greater than 3 in absolute value.

Computation

The orders of variables matters when computing ANCOVA. You want to remove the effect of the covariate first - that is, you want to control for it - prior to entering your main variable or interest.

The covariate goes first (and there is no interaction)! If you do not do this in order, you will get different results.

res.aov <- anxiety %>% anova_test(posttest ~ pretest + group)
get_anova_table(res.aov)

## ANOVA Table (type II tests)
## 
##    Effect DFn DFd   F        p p<.05   ges
## 1 pretest   1  41 598 4.48e-26     * 0.936
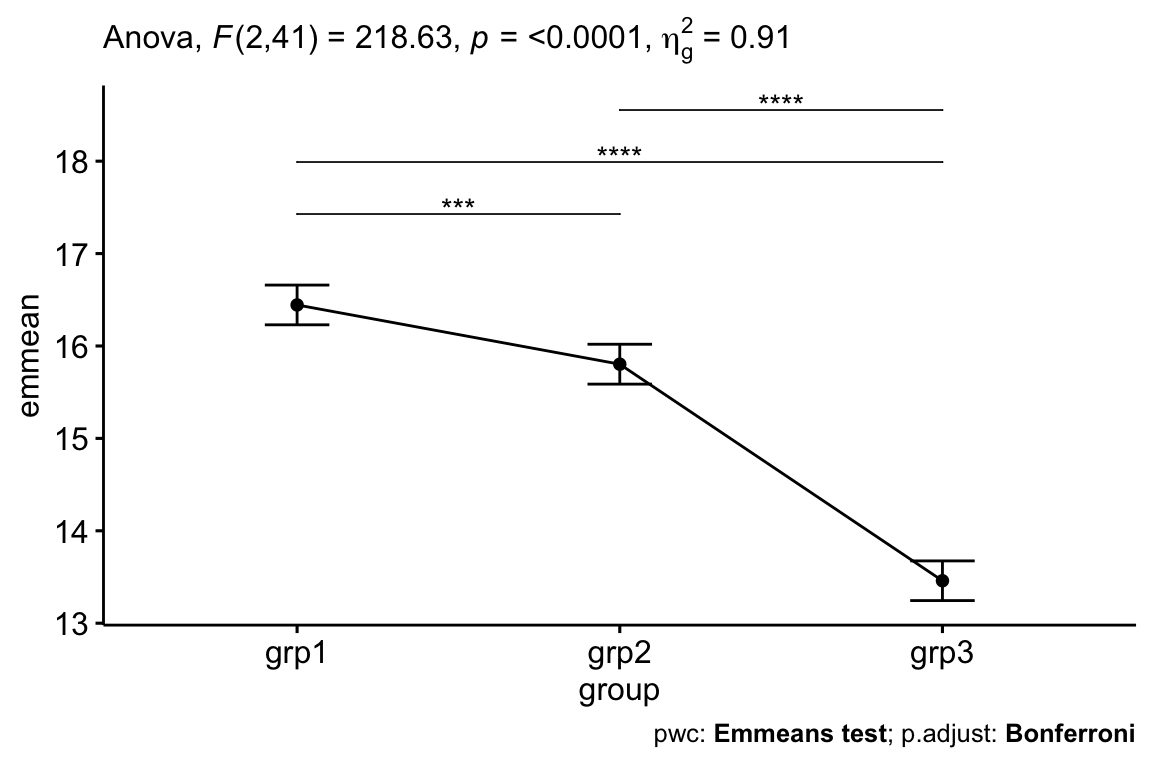
## 2   group   2  41 219 1.35e-22     * 0.914

After adjustment for pre-test anxiety score, there was a statistically significant difference in post-test anxiety score between the groups, F(2, 41) = 218.63, p < 0.0001.

Post-hoc test

Pairwise comparisons can be performed to identify which groups are different. The Bonferroni multiple testing correction is applied. This can be easily done using the function emmeans_test() [rstatix package], a wrapper around the emmeans package, which needs to be installed. Emmeans stands for estimated marginal means (aka least square means or adjusted means).

# Pairwise comparisons
library(emmeans)
pwc <- anxiety %>% 
  emmeans_test(
    posttest ~ group, covariate = pretest,
    p.adjust.method = "bonferroni"
    )
pwc

## # A tibble: 3 x 8
##   .y.      group1 group2    df statistic        p    p.adj p.adj.signif
## * <chr>    <chr>  <chr>  <dbl>     <dbl>    <dbl>    <dbl> <chr>       
## 1 posttest grp1   grp2      41      4.24 1.26e- 4 3.77e- 4 ***         
## 2 posttest grp1   grp3      41     19.9  1.19e-22 3.58e-22 ****        
## 3 posttest grp2   grp3      41     15.5  9.21e-19 2.76e-18 ****

# Display the adjusted means of each group
# Also called as the estimated marginal means (emmeans)
get_emmeans(pwc)

## # A tibble: 3 x 8
##   pretest group emmean    se    df conf.low conf.high method      
##     <dbl> <fct>  <dbl> <dbl> <dbl>    <dbl>     <dbl> <chr>       
## 1    16.9 grp1    16.4 0.106    41     16.2      16.7 Emmeans test
## 2    16.9 grp2    15.8 0.107    41     15.6      16.0 Emmeans test
## 3    16.9 grp3    13.5 0.106    41     13.2      13.7 Emmeans test

Data are adjusted mean +/- standard error. The mean anxiety score was statistically significantly greater in grp1 (16.4 +/- 0.15) compared to the grp2 (15.8 +/- 0.12) and grp3 (13.5 +/_ 0.11), p < 0.001.

Report

An ANCOVA was run to determine the effect of exercises on the anxiety score after controlling for basal anxiety score of participants.

After adjustment for pre-test anxiety score, there was a statistically significant difference in post-test anxiety score between the groups, F(2, 41) = 218.63, p < 0.0001.

Post hoc analysis was performed with a Bonferroni adjustment. The mean anxiety score was statistically significantly greater in grp1 (16.4 +/- 0.15) compared to the grp2 (15.8 +/- 0.12) and grp3 (13.5 +/_ 0.11), p < 0.001.

# Visualization: line plots with p-values
pwc <- pwc %>% add_xy_position(x = "group", fun = "mean_se")
ggline(get_emmeans(pwc), x = "group", y = "emmean") +
  geom_errorbar(aes(ymin = conf.low, ymax = conf.high), width = 0.2) + 
  stat_pvalue_manual(pwc, hide.ns = TRUE, tip.length = FALSE) +
  labs(
    subtitle = get_test_label(res.aov, detailed = TRUE),
    caption = get_pwc_label(pwc)
  )

Two-way ANCOVA

Data preparation

We’ll use the stress dataset available in the datarium package. In this study, a researcher wants to evaluate the effect of treatment and exercise on stress reduction score after adjusting for age.

In this example: 1) stress score is our outcome (dependent) variable; 2) treatment (levels: no and yes) and exercise (levels: low, moderate and high intensity training) are our grouping variable; 3) age is our covariate.

Load the data and show some random rows by groups:

data("stress", package = "datarium")
stress %>% sample_n_by(treatment, exercise)

## # A tibble: 6 x 5
##      id score treatment exercise   age
##   <int> <dbl> <fct>     <fct>    <dbl>
## 1     8  83.8 yes       low         61
## 2    15  86.9 yes       moderate    55
## 3    29  71.5 yes       high        55
## 4    40  92.4 no        low         67
## 5    41 100   no        moderate    75
## 6    56  82.4 no        high        53

Check assumptions

Linearity assumption

Create a scatter plot between the covariate (i.e., age) and the outcome variable (i.e., score) for each combination of the groups of the two grouping variables:
Add smoothed loess lines, which helps to decide if the relationship is linear or not

ggscatter(
  stress, x = "age", y = "score",
  facet.by  = c("exercise", "treatment"), 
  short.panel.labs = FALSE
  )+
  stat_smooth(method = "loess", span = 0.9)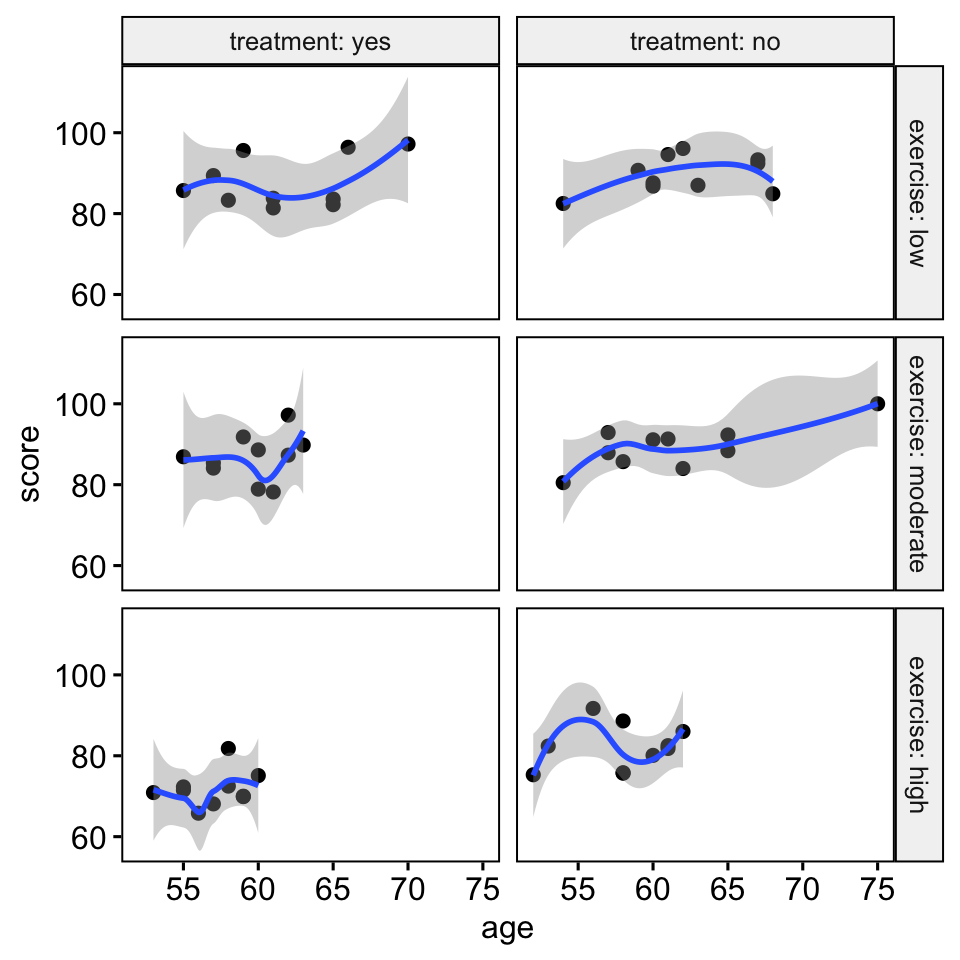

There was a linear relationship between the covariate (age variable) and the outcome variable (score) for each group, as assessed by visual inspection of a scatter plot.

Homogeneity of regression slopes

This assumption checks that there is no significant interaction between the covariate and the grouping variables. This can be evaluated as follow:

stress %>%
  anova_test(
    score ~ age + treatment + exercise + 
     treatment*exercise + age*treatment +
     age*exercise + age*exercise*treatment
  )

## ANOVA Table (type II tests)
## 
##                   Effect DFn DFd      F        p p<.05      ges
## 1                    age   1  48  8.359 6.00e-03     * 0.148000
## 2              treatment   1  48  9.907 3.00e-03     * 0.171000
## 3               exercise   2  48 18.197 1.31e-06     * 0.431000
## 4     treatment:exercise   2  48  3.303 4.50e-02     * 0.121000
## 5          age:treatment   1  48  0.009 9.25e-01       0.000189
## 6           age:exercise   2  48  0.235 7.91e-01       0.010000
## 7 age:treatment:exercise   2  48  0.073 9.30e-01       0.003000

Another simple alternative is to create a new grouping variable, say group, based on the combinations of the existing variables, and then compute ANOVA model:

stress %>%
  unite(col = "group", treatment, exercise) %>%
  anova_test(score ~ group*age)

## ANOVA Table (type II tests)
## 
##      Effect DFn DFd      F        p p<.05   ges
## 1     group   5  48 10.912 4.76e-07     * 0.532
## 2       age   1  48  8.359 6.00e-03     * 0.148
## 3 group:age   5  48  0.126 9.86e-01       0.013

There was homogeneity of regression slopes as the interaction terms, between the covariate (age) and grouping variables (treatment and exercise), was not statistically significant, p > 0.05.

Normality of residuals

# Fit the model, the covariate goes first
model <- lm(score ~ age + treatment*exercise, data = stress)
# Inspect the model diagnostic metrics
model.metrics <- augment(model) %>%
  select(-.hat, -.sigma, -.fitted, -.se.fit) # Remove details
head(model.metrics, 3)

## # A tibble: 3 x 7
##   score   age treatment exercise .resid .cooksd .std.resid
##   <dbl> <dbl> <fct>     <fct>     <dbl>   <dbl>      <dbl>
## 1  95.6    59 yes       low        9.10  0.0647       1.93
## 2  82.2    65 yes       low       -7.32  0.0439      -1.56
## 3  97.2    70 yes       low        5.16  0.0401       1.14

# Assess normality of residuals using shapiro wilk test
shapiro_test(model.metrics$.resid)

## # A tibble: 1 x 3
##   variable             statistic p.value
##   <chr>                    <dbl>   <dbl>
## 1 model.metrics$.resid     0.982   0.531

The Shapiro Wilk test was not significant (p > 0.05), so we can assume normality of residuals

Homogeneity of variances

ANCOVA assumes that the variance of the residuals is equal for all groups. This can be checked using the Levene’s test:

levene_test(.resid ~ treatment*exercise, data = model.metrics)

The Levene’s test was not significant (p > 0.05), so we can assume homogeneity of the residual variances for all groups.

Outliers

Observations whose standardized residuals are greater than 3 in absolute value are possible outliers.

model.metrics %>% 
  filter(abs(.std.resid) > 3) %>%
  as.data.frame()

## [1] score      age        treatment  exercise   .resid     .cooksd    .std.resid
## <0 rows> (or 0-length row.names)

There were no outliers in the data, as assessed by no cases with standardized residuals greater than 3 in absolute value.

Computation

res.aov <- stress %>% 
  anova_test(score ~ age + treatment*exercise)
get_anova_table(res.aov)

## ANOVA Table (type II tests)
## 
##               Effect DFn DFd     F        p p<.05   ges
## 1                age   1  53  9.11 4.00e-03     * 0.147
## 2          treatment   1  53 11.10 2.00e-03     * 0.173
## 3           exercise   2  53 20.82 2.13e-07     * 0.440
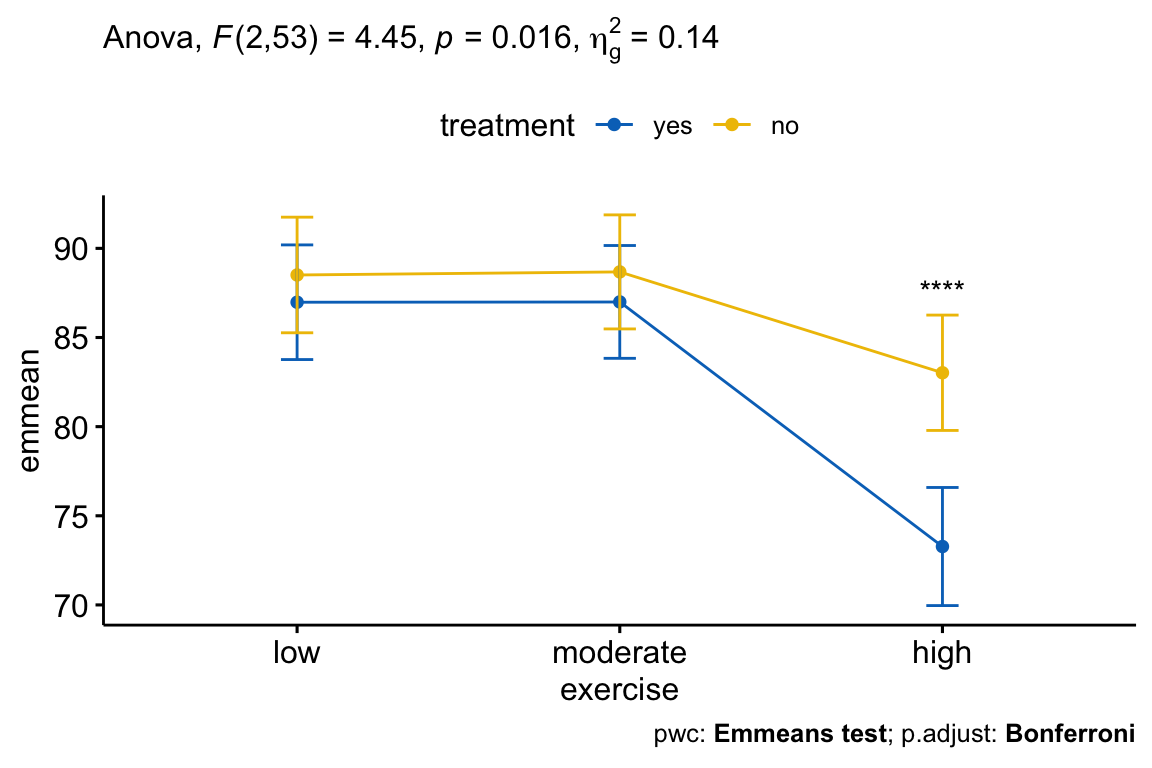
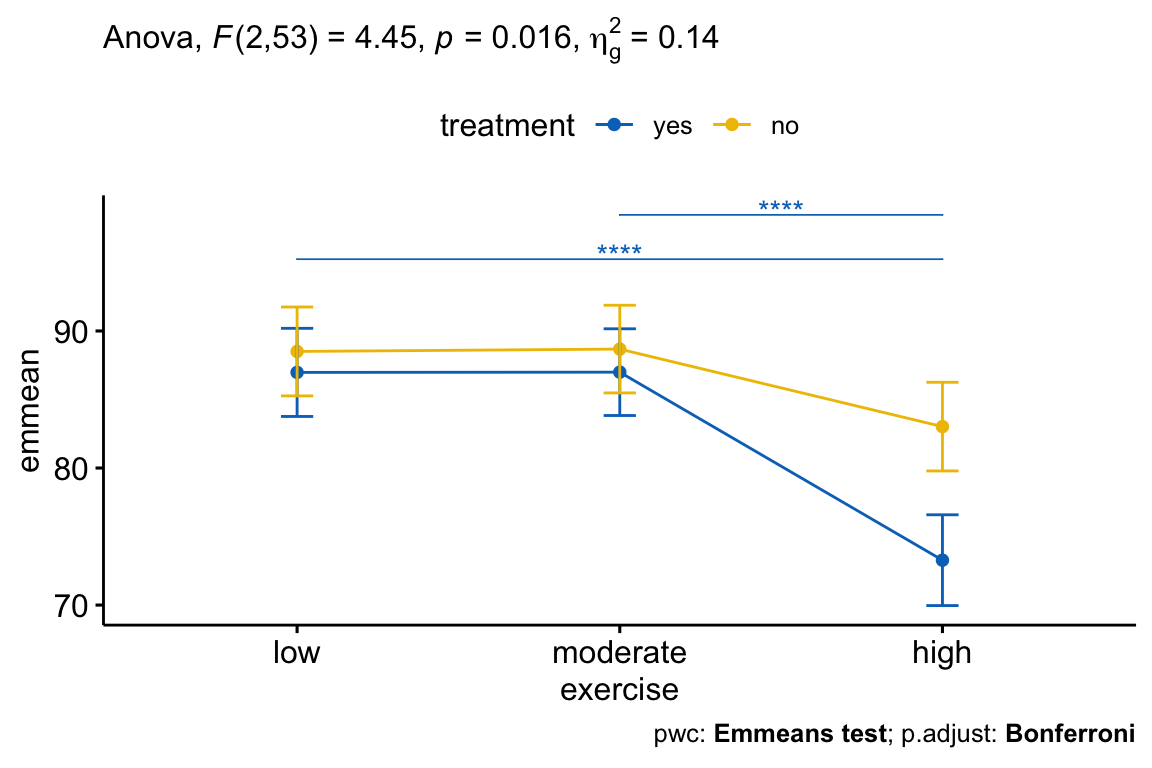
## 4 treatment:exercise   2  53  4.45 1.60e-02     * 0.144

After adjustment for age, there was a statistically significant interaction between treatment and exercise on the stress score, F(2, 53) = 4.45, p = 0.016. This indicates that the effect of exercise on score depends on the level of exercise, and vice-versa.

Post-hoc test

A statistically significant two-way interactions can be followed up by simple main effect analyses, that is evaluating the effect of one variable at each level of the second variable, and vice-versa.

In the situation, where the interaction is not significant, you can report the main effect of each grouping variable.

A significant two-way interaction indicates that the impact that one factor has on the outcome variable depends on the level of the other factor (and vice versa). So, you can decompose a significant two-way interaction into:

Simple main effect: run one-way model of the first variable (factor A) at each level of the second variable (factor B),
Simple pairwise comparisons: if the simple main effect is significant, run multiple pairwise comparisons to determine which groups are different.

For a non-significant two-way interaction, you need to determine whether you have any statistically significant main effects from the ANCOVA output.

In this section we’ll describe the procedure for a significant three-way interaction

Simple main effect analyses for treatment

Analyze the simple main effect of treatment at each level of exercise. Group the data by exercise and perform one-way ANCOVA for treatment controlling for age:

# Effect of treatment at each level of exercise
stress %>%
  group_by(exercise) %>%
  anova_test(score ~ age + treatment)

## # A tibble: 6 x 8
##   exercise Effect      DFn   DFd      F        p `p<.05`   ges
##   <fct>    <chr>     <dbl> <dbl>  <dbl>    <dbl> <chr>   <dbl>
## 1 low      age           1    17  2.25  0.152    ""      0.117
## 2 low      treatment     1    17  0.437 0.517    ""      0.025
## 3 moderate age           1    17  6.65  0.02     *       0.281
## 4 moderate treatment     1    17  0.419 0.526    ""      0.024
## 5 high     age           1    17  0.794 0.385    ""      0.045
## 6 high     treatment     1    17 18.7   0.000455 *       0.524

Note that, we need to apply Bonferroni adjustment for multiple testing corrections. One common approach is lowering the level at which you declare significance by dividing the alpha value (0.05) by the number of tests performed. In our example, that is 0.05/3 = 0.016667.

Statistical significance was accepted at the Bonferroni-adjusted alpha level of 0.01667, that is 0.05/3. The effect of treatment was statistically significant in the high-intensity exercise group (p = 0.00045), but not in the low-intensity exercise group (p = 0.517) and in the moderate-intensity exercise group (p = 0.526).

Compute pairwise comparisons between treatment groups at each level of exercise. The Bonferroni multiple testing correction is applied.

# Pairwise comparisons
pwc <- stress %>% 
  group_by(exercise) %>%
  emmeans_test(
    score ~ treatment, covariate = age,
    p.adjust.method = "bonferroni"
    )
pwc %>% filter(exercise == "high")

## # A tibble: 1 x 9
##   exercise .y.   group1 group2    df statistic         p     p.adj p.adj.signif
##   <fct>    <chr> <chr>  <chr>  <dbl>     <dbl>     <dbl>     <dbl> <chr>       
## 1 high     score yes    no        53     -4.36 0.0000597 0.0000597 ****

In the pairwise comparison table, you will only need the result for “exercises:high” group, as this was the only condition where the simple main effect of treatment was statistically significant.

The pairwise comparisons between treatment:no and treatment:yes group was statistically significant in participant undertaking high-intensity exercise (p < 0.0001).

Simple main effect for exercise

You can do the same post-hoc analyses for the exercise variable at each level of treatment variable.

# Effect of exercise at each level of treatment
stress %>%
  group_by(treatment) %>%
  anova_test(score ~ age + exercise)

## # A tibble: 4 x 8
##   treatment Effect     DFn   DFd     F         p `p<.05`   ges
##   <fct>     <chr>    <dbl> <dbl> <dbl>     <dbl> <chr>   <dbl>
## 1 yes       age          1    26  2.37 0.136     ""      0.083
## 2 yes       exercise     2    26 17.3  0.0000164 *       0.572
## 3 no        age          1    26  7.26 0.012     *       0.218
## 4 no        exercise     2    26  3.99 0.031     *       0.235

Statistical significance was accepted at the Bonferroni-adjusted alpha level of 0.025, that is 0.05/2 (the number of tests). The effect of exercise was statistically significant in the treatment=yes group (p < 0.0001), but not in the treatment=no group (p = 0.031).

Perform multiple pairwise comparisons between exercise groups at each level of treatment. You don’t need to interpret the results for the “no treatment” group, because the effect of exercise was not significant for this group.

pwc2 <- stress %>% 
  group_by(treatment) %>%
  emmeans_test(
    score ~ exercise, covariate = age,
    p.adjust.method = "bonferroni"
    ) %>%
  select(-df, -statistic, -p) # Remove details
pwc2 %>% filter(treatment == "yes")

## # A tibble: 3 x 6
##   treatment .y.   group1   group2         p.adj p.adj.signif
##   <fct>     <chr> <chr>    <chr>          <dbl> <chr>       
## 1 yes       score low      moderate 1           ns          
## 2 yes       score low      high     0.00000113  ****        
## 3 yes       score moderate high     0.000000466 ****

There was a statistically significant difference between the adjusted mean of low and high exercise group (p < 0.0001) and, between moderate and high group (p < 0.0001). The difference between the adjusted means of low and moderate was not significant.

Report

A two-way ANCOVA was performed to examine the effects of treatment and exercise on stress reduction, after controlling for age.

There was a statistically significant two-way interaction between treatment and exercise on score concentration, whilst controlling for age, F(2, 53) = 4.45, p = 0.016.

Therefore, an analysis of simple main effects for exercise and treatment was performed with statistical significance receiving a Bonferroni adjustment and being accepted at the p < 0.025 level for exercise and p < 0.0167 for treatment.

The simple main effect of treatment was statistically significant in the high-intensity exercise group (p = 0.00046), but not in the low-intensity exercise group (p = 0.52) and the moderate-intensity exercise group (p = 0.53).

The effect of exercise was statistically significant in the treatment=yes group (p < 0.0001), but not in the treatment=no group (p = 0.031).

All pairwise comparisons were computed for statistically significant simple main effects with reported p-values Bonferroni adjusted. For the treatment=yes group, there was a statistically significant difference between the adjusted mean of low and high exercise group (p < 0.0001) and, between moderate and high group (p < 0.0001). The difference between the adjusted means of low and moderate exercise groups was not significant.

Create a line plot:

# Line plot
lp <- ggline(
  get_emmeans(pwc), x = "exercise", y = "emmean", 
  color = "treatment", palette = "jco"
  ) +
  geom_errorbar(
    aes(ymin = conf.low, ymax = conf.high, color = treatment), 
    width = 0.1
    )

Add p-values

# Comparisons between treatment group at each exercise level
pwc <- pwc %>% add_xy_position(x = "exercise", fun = "mean_se", step.increase = 0.2)
pwc.filtered <- pwc %>% filter(exercise == "high")
lp + 
stat_pvalue_manual(
  pwc.filtered, hide.ns = TRUE, tip.length = 0,
  bracket.size = 0
  ) +
labs(
  subtitle = get_test_label(res.aov,  detailed = TRUE),
  caption = get_pwc_label(pwc)
)

# Comparisons between exercises group at each treatment level
pwc2 <- pwc2 %>% add_xy_position(x = "exercise", fun = "mean_se")
pwc2.filtered <- pwc2 %>% filter(treatment == "yes")
lp + 
stat_pvalue_manual(
  pwc2.filtered, hide.ns = TRUE, tip.length = 0,
  step.group.by = "treatment", color = "treatment"
  ) +
labs(
  subtitle = get_test_label(res.aov,  detailed = TRUE),
  caption = get_pwc_label(pwc2)
)

Summary

This article describes how to compute and interpret one-way and two-way ANCOVA in R. We also explain the assumptions made by ANCOVA tests and provide practical examples of R codes to check whether the test assumptions are met or not.

Recommended for you

This section contains best data science and self-development resources to help you on your path.

Coursera - Online Courses and Specialization

Amazon FBA

Amazing Selling Machine

Free Training - How to Build a 7-Figure Amazon FBA Business You Can Run 100% From Home and Build Your Dream Life! by ASM

Books - Data Science

Our Books

Practical Guide to Cluster Analysis in R by A. Kassambara (Datanovia)
Practical Guide To Principal Component Methods in R by A. Kassambara (Datanovia)
Machine Learning Essentials: Practical Guide in R by A. Kassambara (Datanovia)
R Graphics Essentials for Great Data Visualization by A. Kassambara (Datanovia)
GGPlot2 Essentials for Great Data Visualization in R by A. Kassambara (Datanovia)
Network Analysis and Visualization in R by A. Kassambara (Datanovia)
Practical Statistics in R for Comparing Groups: Numerical Variables by A. Kassambara (Datanovia)
Inter-Rater Reliability Essentials: Practical Guide in R by A. Kassambara (Datanovia)

Others

R for Data Science: Import, Tidy, Transform, Visualize, and Model Data by Hadley Wickham & Garrett Grolemund
Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurelien Géron
Practical Statistics for Data Scientists: 50 Essential Concepts by Peter Bruce & Andrew Bruce
Hands-On Programming with R: Write Your Own Functions And Simulations by Garrett Grolemund & Hadley Wickham
An Introduction to Statistical Learning: with Applications in R by Gareth James et al.
Deep Learning with R by François Chollet & J.J. Allaire
Deep Learning with Python by François Chollet

Version: Français

Back to Comparing Multiple Means in R

Comments ( 40 )

WAGNER

24 Dec 2019

Codes for line plots were not working

Reply
- Kassambara
  
  25 Dec 2019
  
  Would you indicate the error message?
  
  Reply
  - WAGNER FARIA BARBOSA
    
    06 Mar 2020
    
    Warning: Ignoring unknown parameters: hide.ns
    Warning: Ignoring unknown aesthetics: xmin, xmax, annotations, y_position
    Error in f(…) :
    Can only handle data with groups that are plotted on the x-axis
    
    Reply
    - Kassambara
      
      06 Mar 2020
      
      Make sure you have the latest version of ggpubr and rstatix packages
      
      Reply
Javiera Benavente

14 Jan 2020

Hey, why does the function anova_test() gives different p-values than using the car package function Anova (lm(y~X), Type=II)?. Does it calculate things differently?

Reply
Xiaochi

12 Feb 2020

Hi there. When plotting the test result, I don’t quite understand how to set the “fun” argument in the add_xy_position( ).

In this tutorial, the “fun” argument was set to “mean_se”. However, in the previous ANOVA tutorial, the “fun” argument was set to “max”. And there are other options like “mean_ci”, “mean_sd”, “median”, and so on.

I like those brackets to show the significantly pairwise difference. However, I don’t know the meaning of these brackets’ y.position, and how I should choose the different options.

Looking forward to your response. Thanks!

Reply
- Kassambara
  
  12 Feb 2020
  
  Thank you for your feedback!
  
  When the main plot is a boxplot, you need the option fun = “max” to have the bracket displayed at the maximum point of the group
  
  In some situations the main plot is a line plot or a barplot showing the mean+/-error of tgroups, where error can be SE (standard error), SD (standard deviation) or CI (confidence interval). In this case, to correctly compute the bracket y position you need the option fun = “mean_se”, etc
  
  Hope, this clarifies a bit the usage of the option “fun”
  Thanks!
  
  Reply
Macs

13 Feb 2020

Really nice walkthrough! Thank you! I’m having some trouble running the 2-way ANCOVA; similar setup where my outcome and covariate are numerical and my grouping factors have 2 and 3 levels each:
MRacov %
anova_test(SLIPSPEED ~ FKL + SPECIESID*AUG)
Error in `contrasts<-`(`*tmp*`, value = contr.funs[1 + isOF[nn]]) : contrasts can be applied only to factors with 2 or more levels

Reply
- Macs
  
  14 Feb 2020
  
  Hi so sorry, I had a couple irrelevant columns containing NAs. Once I removed those columns it worked just fine!!
  
  Reply
Chau

21 Feb 2020

Hello,
Can a different method of p-value adjust be used, other than Bonferroni with this package? I’m looking for adjusted p-value for multiple comparisons such as BH and BY:

The “BH” (aka “fdr”) and “BY” method of Benjamini, Hochberg, and Yekutieli control the false discovery rate, the expected proportion of false discoveries amongst the rejected hypotheses. The false discovery rate is a less stringent condition than the family-wise error rate, so these methods are more powerful than the others.

Reply
- Kassambara
  
  21 Feb 2020
  
  yes, you just need to specify “BH” when using the function
  
  Reply
Lucas Rodrigues Tovar

20 Apr 2020

When I try run the emmeans test de output is this erros message:
Error in contrast.emmGrid(res.emmeans, by = grouping.vars, method = method, :
Nonconforming number of contrast coefficients

I have three variables, two categorical (one binary and the other have four values) and one more numeric varible. I would be very happy having this working

Reply
- Kassambara
  
  20 Apr 2020
  
  Would you please provide a reproducible exampleas described at https://www.datanovia.com/en/blog/publish-reproducible-examples-from-r-to-datanovia-website/
  
  Reply
Chris

01 May 2020

Continuous trouble when running the ANCOVA report plot, I seem to get the following message:
“Error in `[.data.frame`(data, , x) : undefined columns selected”

Reply
- Kassambara
  
  02 May 2020
  
  Please provide a reproducible script with a demo data so that I can help
  
  Reply
  - Chris
    
    04 May 2020
    
    Thanks Kassambara. I have just began trying to provide a reproducible script and see that the required package ‘pub’ is not available in R v 4.0. Is there an alternative package that can be used for this? thanks, Chris
    
    Reply
    - Kassambara
      
      04 May 2020
      
      Hi Chris, Is the installation procedure works as described at https://www.datanovia.com/en/blog/publish-reproducible-examples-from-r-to-datanovia-website/ ?
      
      Reply
Sam

05 Jun 2020

In the report there is no description for pairwise comparisons between treatment:no and treatment:yes group was statistically significant in participant undertaking high-intensity exercise (p < 0.0001). Why?

Reply
Barb

30 Jun 2020

Given a similar problem of value~time+group, how would you evaluate the differences between groups when the Shapiro Wilk test results in p<0.05?

Reply
Lauren

17 Jul 2020

When running the visualization, I continue to get the following error:

Error in stop_ifnot_class(stat.test, .class = names(allowed.tests)) :
stat.test should be an object of class: t_test, wilcox_test, sign_test, dunn_test, emmeans_test, tukey_hsd, games_howell_test, prop_test, fisher_test, chisq_test, exact_binom_test, mcnemar_test, kruskal_test, friedman_test, anova_test, welch_anova_test, chisq_test, exact_multinom_test, exact_binom_test, cochran_qtest, chisq_trend_test

Reply
- Kassambara
  
  18 Jul 2020
  
  It works on my computer. Please make sure you have the latest version of rstatix and ggpubr r packages.
  
  Reply
  - George
    
    04 Feb 2021
    
    I had the same problem even after updating all packages. Additionally, emmeans_test report an error:
    Error: Column name `std. error` must not be duplicated. Before updating, It worked.
    
    Reply
- Nixon
  
  26 Jun 2021
  
  Hello Lauren, have you been able to fix it? Thanks for advance.
  
  Reply
Emma

29 Jul 2020

In the outlier test section you say that standardized residuals are residuals divided by standard error. I though they were residuals divided by standard deviation.

Reply
Lucas Tovar

09 Aug 2020

When i run the emmeans test whatever method i but the significance adjusted do not change

Reply
Alex

03 Sep 2020

Hi, thanks for this tutorial. When running the demo data exactly as presented in this example, I get the following error:

model.metrics %
select(-.hat, -.sigma, -.fitted, -.se.fit) # Remove details

Error: Can’t subset columns that don’t exist.
x Column `.se.fit` doesn’t exist.

Can you tell me how to fix this? Thanks.

Reply
- James
  
  23 Nov 2020
  
  me too!
  
  Reply
  - Kelsey
    
    06 Jan 2021
    
    me too!
    
    Reply
- Miguel
  
  31 Mar 2021
  
  After several hours looking for an answer without success, I tried trial and error…
  Just remove the argument “-.se.fit”
  It worked for me
  
  Reply
Pablo

25 Nov 2020

Thank you very much for sharing this! I am trying to include several covariates in the Pairwise comparisons of one-way ANCOVA but I cannot manage it. Could you help me with that?

Reply
Shai Posat

31 Dec 2020

This is a random sample of my data set:

“`
structure(list(DTI_ID = structure(c(31L, 241L, 84L, 298L, 185L,
269L, 198L, 24L, 286L, 177L, 228L, 158L, 57L, 293L, 218L, 8L,
180L, 39L, 211L, 134L, 291L, 309L, 99L, 70L, 154L, 138L, 250L,
41L, 276L, 262L, 96L, 139L, 232L, 12L, 294L, 38L, 244L, 289L,
280L, 196L, 58L, 44L, 188L, 152L, 143L, 302L, 201L, 27L, 24L,
67L, 247L, 223L, 74L, 32L, 110L, 98L, 303L, 256L, 71L, 30L, 236L,
266L, 307L, 224L, 100L, 73L, 288L, 230L, 182L, 159L, 190L, 123L,
241L, 169L, 103L, 40L, 248L, 293L, 60L, 260L, 168L, 267L, 144L,
89L, 139L, 231L, 204L, 130L, 278L, 227L, 205L, 268L, 88L, 221L,
208L, 306L, 242L, 145L, 21L, 165L, 217L, 159L, 206L, 70L, 121L,
181L, 95L, 279L, 265L, 4L, 122L, 177L, 234L, 34L, 261L, 86L,
2L, 296L, 39L, 283L, 251L, 126L, 188L, 176L, 220L, 77L, 225L,
73L, 48L, 107L, 280L, 118L, 38L, 310L, 297L, 258L, 89L, 205L,
4L, 54L, 16L, 95L, 119L, 40L, 9L, 66L, 64L, 55L, 131L, 290L,
166L, 170L, 182L, 139L, 125L, 201L, 302L, 137L, 8L, 81L, 61L,
119L, 278L, 135L, 117L, 65L, 21L, 200L, 150L, 146L, 54L, 262L,
152L, 224L, 162L, 111L, 251L, 130L, 41L, 271L, 33L, 86L, 32L,
199L, 49L, 180L, 101L, 271L, 80L, 84L, 293L, 5L, 170L, 74L, 279L,
281L, 255L, 210L, 52L, 248L, 53L, 121L, 190L, 141L, 213L, 138L,
112L, 234L, 235L, 40L, 233L, 115L, 154L, 11L, 76L, 29L, 19L,
249L, 1L, 207L), .Label = c(“5356”, “5357”, “5358”, “5359”, “5360”,
“5363”, “5373”, “5381”, “5383”, “5386”, “5395”, “5397”, “5400”,
“5401”, “5444”, “5445”, “5446”, “5448”, “5450”, “5451”, “5454”,
“5472”, “5473”, “5475”, “5476”, “5477”, “5478”, “5480”, “5481”,
“5483”, “5487”, “5494”, “5495”, “5504”, “5505”, “5506”, “5507”,
“5508”, “5509”, “5513”, “5514”, “5515”, “5516”, “5517”, “5518”,
“5519”, “5521”, “5523”, “5524”, “5526”, “5527”, “5528”, “5544”,
“5545”, “5546”, “5547”, “5551”, “5552”, “5553”, “5554”, “5555”,
“5558”, “5559”, “5560”, “5562”, “5564”, “5566”, “5573”, “5574”,
“5575”, “5576”, “5577”, “5578”, “5579”, “5584”, “5585”, “5587”,
“5588”, “5589”, “5591”, “5594”, “5595”, “5604”, “5611”, “5612”,
“5613”, “5615”, “5616”, “5619”, “5620”, “5621”, “5622”, “5626”,
“5627”, “5628”, “5631”, “5632”, “5634”, “5635”, “5643”, “5652”,
“5653”, “5654”, “5655”, “5656”, “5657”, “5659”, “5660”, “5661”,
“5664”, “5665”, “5666”, “5669”, “5671”, “5672”, “5673”, “5678”,
“5680”, “5688”, “5689”, “5690”, “5691”, “5692”, “5698”, “5699”,
“5700”, “5702”, “5703”, “5704”, “5706”, “5708”, “5709”, “5710”,
“5730”, “5731”, “5732”, “5733”, “5734”, “5735”, “5739”, “5740”,
“5741”, “5742”, “5743”, “5744”, “5745”, “5746”, “5747”, “5748”,
“5749”, “5750”, “5753”, “5754”, “5755”, “5766”, “5767”, “5776”,
“5777”, “5778”, “5779”, “5780”, “5781”, “5787”, “5788”, “5789”,
“5790”, “5791”, “5792”, “5793”, “5797”, “5798”, “5799”, “5800”,
“5801”, “5810”, “5811”, “5812”, “5813”, “5814”, “5819”, “5820”,
“5821”, “5822”, “5823”, “5824”, “5825”, “5827”, “5828”, “5829”,
“5830”, “5857”, “5859”, “5874”, “5875”, “5876”, “5877”, “5878”,
“5879”, “5883”, “5884”, “5886”, “5887”, “5888”, “5889”, “5890”,
“5892”, “5893”, “5896”, “5899”, “5900”, “5909”, “5910”, “5918”,
“5919”, “5920”, “5921”, “5922”, “5923”, “5927”, “5929”, “5931”,
“5932”, “5933”, “5934”, “5936”, “5937”, “5941”, “5943”, “5944”,
“5949”, “5950”, “5951”, “5952”, “5956”, “5957”, “5958”, “5959”,
“5971”, “5972”, “5973”, “5976”, “5979”, “5980”, “5981”, “6001”,
“6002”, “6003”, “6004”, “6005”, “6009”, “6027”, “6028”, “6033”,
“6042”, “6054”, “6063”, “6067”, “6073”, “6076”, “6077”, “6078”,
“6079”, “6080”, “6081”, “6082”, “6083”, “6098”, “6102”, “6103”,
“6104”, “6105”, “6106”, “6107”, “6111”, “6119”, “6133”, “6146”,
“6147”, “6157”, “6158”, “6160”, “6161”, “6162”, “6163”, “6164”,
“6165”, “6166”, “6167”, “6168”, “6169”, “6170”, “6171”, “6172”,
“6173”, “6174”, “6175”, “6190”, “6193”, “6195”, “6196”, “6197”,
“6208”, “6228”, “6229”, “6232”, “6255”, “6268”, “6269”, “6270”,
“6275”), class = “factor”), Gender = structure(c(2L, 2L, 1L,
2L, 2L, 1L, 2L, 1L, 1L, 1L, 1L, 1L, 1L, 2L, 1L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 1L,
1L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 1L, 2L, 2L, 1L, 2L, 1L, 2L, 1L,
2L, 2L, 2L, 1L, 2L, 1L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 1L, 1L,
2L, 2L, 2L, 1L, 2L, 2L, 2L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 1L, 1L,
2L, 2L, 2L, 2L, 1L, 2L, 1L, 1L, 1L, 2L, 2L, 1L, 1L, 2L, 2L, 2L,
1L, 1L, 2L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 1L, 2L, 1L,
2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L,
2L, 1L, 1L, 2L, 2L, 2L, 1L, 2L, 1L, 2L, 2L, 2L, 1L, 2L, 2L, 1L,
1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 1L, 2L, 2L, 2L, 2L, 1L, 2L, 1L, 2L, 2L, 2L, 2L, 1L, 2L,
2L, 2L, 2L, 2L, 2L, 1L, 2L, 1L, 2L, 1L, 1L, 2L, 2L, 2L, 2L, 2L,
2L, 1L, 2L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 2L, 2L, 1L, 2L, 1L, 2L,
1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 1L), .Label = c(“Female”, “Male”
), class = “factor”), Age = structure(c(2L, 1L, 2L, 2L, 2L, 2L,
1L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 1L, 1L, 2L,
2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L,
1L, 1L, 1L, 2L, 2L, 2L, 1L, 2L, 1L, 2L, 2L, 2L, 1L, 1L, 2L, 1L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L,
2L, 2L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 1L, 1L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L,
2L, 1L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L,
2L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 1L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 1L, 2L, 2L), .Label = c(“Young”, “Old”), class = “factor”),
ROI = structure(c(4L, 4L, 1L, 2L, 3L, 3L, 3L, 2L, 2L, 1L,
3L, 2L, 4L, 1L, 1L, 2L, 4L, 4L, 1L, 4L, 4L, 4L, 1L, 1L, 4L,
2L, 1L, 2L, 2L, 2L, 4L, 1L, 1L, 3L, 3L, 3L, 4L, 3L, 1L, 4L,
2L, 2L, 3L, 4L, 2L, 2L, 1L, 2L, 3L, 1L, 4L, 4L, 3L, 4L, 4L,
1L, 3L, 4L, 3L, 3L, 1L, 3L, 1L, 1L, 1L, 4L, 2L, 1L, 4L, 3L,
2L, 2L, 3L, 4L, 1L, 2L, 1L, 4L, 2L, 1L, 3L, 1L, 2L, 2L, 4L,
1L, 1L, 4L, 4L, 3L, 1L, 2L, 1L, 1L, 2L, 2L, 1L, 4L, 4L, 1L,
2L, 4L, 1L, 2L, 2L, 3L, 4L, 1L, 2L, 3L, 4L, 4L, 3L, 2L, 4L,
1L, 1L, 3L, 3L, 3L, 1L, 2L, 4L, 3L, 4L, 1L, 4L, 3L, 2L, 1L,
4L, 4L, 4L, 2L, 4L, 1L, 4L, 2L, 1L, 3L, 1L, 2L, 3L, 3L, 3L,
1L, 1L, 2L, 4L, 4L, 1L, 4L, 1L, 3L, 3L, 4L, 1L, 3L, 4L, 2L,
2L, 1L, 1L, 1L, 1L, 4L, 1L, 4L, 1L, 4L, 2L, 4L, 3L, 3L, 3L,
2L, 2L, 2L, 1L, 4L, 4L, 3L, 3L, 4L, 3L, 1L, 4L, 2L, 2L, 3L,
2L, 3L, 1L, 2L, 3L, 2L, 1L, 3L, 3L, 2L, 4L, 1L, 1L, 2L, 1L,
4L, 4L, 1L, 2L, 1L, 2L, 4L, 2L, 4L, 1L, 4L, 2L, 4L, 3L, 2L
), .Label = c(“A”, “B”,”C”, “D”), class = “factor”),
value = c(0.326713741, 0.349206239, 0.365954667,
0.313958377, 0.480487555, 0.431199849, 0.446729183, 0.337009728,
0.331222087, 0.386937141, 0.372758657, 0.305083066, 0.504718482,
0.414191663, 0.40949735, 0.271525055, 0.30009532, 0.50117749,
0.387669057, 0.330797315, 0.390679717, 0.452181876, 0.423188657,
0.396808296, 0.388510793, 0.298505336, 0.412985921, 0.327000797,
0.304242313, 0.277513236, 0.394773901, 0.4322685, 0.440891623,
0.439061254, 0.453015536, 0.385896087, 0.452299237, 0.296923041,
0.443324417, 0.420699686, 0.282610774, 0.303566545, 0.535346806,
0.393591255, 0.32561186, 0.309230596, 0.417596817, 0.281766504,
0.445347071, 0.353419632, 0.354420125, 0.429613769, 0.385733992,
0.155136898, 0.485385537, 0.439544022, 0.436584443, 0.458706915,
0.600399196, 0.440390527, 0.362952292, 0.37253055, 0.37306264,
0.371298164, 0.469741255, 0.573943496, 0.283266962, 0.391182601,
0.663566113, 0.517713368, 0.327498972, 0.353969425, 0.443648636,
0.449972481, 0.434426159, 0.305042148, 0.422493547, 0.194572225,
0.331083208, 0.418288261, 0.447215647, 0.429001331, 0.339149892,
0.336879104, 0.471237898, 0.408330619, 0.393405557, 0.486086488,
0.427713692, 0.379242182, 0.40456596, 0.326695889, 0.393235713,
0.452374548, 0.332855165, 0.323469192, 0.396484613, 0.372199923,
0.257353246, 0.405249774, 0.326494843, 0.420468688, 0.335335255,
0.267627925, 0.379383296, 0.338241786, 0.416064918, 0.381003618,
0.284006208, 0.442705005, 0.494199812, 0.464447916, 0.370418996,
0.293953657, 0.34482345, 0.47208631, 0.378798842, 0.407261223,
0.34767586, 0.424341202, 0.434532404, 0.342623293, 0.628901243,
0.381492049, 0.540111601, 0.392371207, 0.459349483, 0.373172134,
0.270272404, 0.413454324, 0.375994682, 0.470298111, 0.340463549,
0.31613645, 0.470312864, 0.410651028, 0.276164204, 0.341546267,
0.402167588, 0.465735435, 0.434102625, 0.328114063, 0.394582212,
0.331681252, 0.387562275, 0.3989245, 0.44939962, 0.29586333,
0.398924828, 0.559520543, 0.392099082, 0.589552164, 0.397368163,
0.375135392, 0.348508835, 0.447002649, 0.407775551, 0.404435992,
0.666776299, 0.265039146, 0.25311482, 0.354386091, 0.44051528,
0.416727781, 0.460624784, 0.455415428, 0.445090771, 0.502343714,
0.393426061, 0.463244319, 0.345586747, 0.291874498, 0.564393103,
0.400276631, 0.41512531, 0.308440536, 0.373545259, 0.272377819,
0.434890926, 0.358394623, 0.414819628, 0.761894882, 0.409700364,
0.403811544, 0.469092041, 0.397044837, 0.312479883, 0.294876397,
0.314414322, 0.428720832, 0.329074681, 0.311423391, 0.444689006,
0.254723012, 0.248710752, 0.270434052, 0.416304022, 0.38875562,
0.396840513, 0.296386898, 0.454476953, 0.474986047, 0.427072734,
0.270839244, 0.426266223, 0.586857438, 0.348018169, 0.386638522,
0.349321723, 0.418692261, 0.295630395, 0.463439822, 0.286190838,
0.336389571, 0.422766507, 0.231764346, 0.358636618, 0.562871873,
0.381515294, 0.28637746)), row.names = c(961L, 1171L, 84L,
608L, 805L, 889L, 818L, 334L, 596L, 177L, 848L, 468L, 987L, 293L,
218L, 318L, 1110L, 969L, 211L, 1064L, 1221L, 1239L, 99L, 70L,
1084L, 448L, 250L, 351L, 586L, 572L, 1026L, 139L, 232L, 632L,
914L, 658L, 1174L, 909L, 280L, 1126L, 368L, 354L, 808L, 1082L,
453L, 612L, 201L, 337L, 644L, 67L, 1177L, 1153L, 694L, 962L,
1040L, 98L, 923L, 1186L, 691L, 650L, 236L, 886L, 307L, 224L,
100L, 1003L, 598L, 230L, 1112L, 779L, 500L, 433L, 861L, 1099L,
103L, 350L, 248L, 1223L, 370L, 260L, 788L, 267L, 454L, 399L,
1069L, 231L, 204L, 1060L, 1208L, 847L, 205L, 578L, 88L, 221L,
518L, 616L, 242L, 1075L, 951L, 165L, 527L, 1089L, 206L, 380L,
431L, 801L, 1025L, 279L, 575L, 624L, 1052L, 1107L, 854L, 344L,
1191L, 86L, 2L, 916L, 659L, 903L, 251L, 436L, 1118L, 796L, 1150L,
77L, 1155L, 693L, 358L, 107L, 1210L, 1048L, 968L, 620L, 1227L,
258L, 1019L, 515L, 4L, 674L, 16L, 405L, 739L, 660L, 629L, 66L,
64L, 365L, 1061L, 1220L, 166L, 1100L, 182L, 759L, 745L, 1131L,
302L, 757L, 938L, 391L, 371L, 119L, 278L, 135L, 117L, 995L, 21L,
1130L, 150L, 1076L, 364L, 1192L, 772L, 844L, 782L, 421L, 561L,
440L, 41L, 1201L, 963L, 706L, 652L, 1129L, 669L, 180L, 1031L,
581L, 390L, 704L, 603L, 625L, 170L, 384L, 899L, 591L, 255L, 830L,
672L, 558L, 983L, 121L, 190L, 451L, 213L, 1068L, 1042L, 234L,
545L, 40L, 543L, 1045L, 464L, 941L, 76L, 959L, 329L, 1179L, 621L,
517L), class = “data.frame”)
“`
Which looks like:

“`
# A tibble: 10 x 5
DTI_ID Gender Age ROI value

1 5927 Male Old A 0.395
2 5634 Male Old C 0.433
3 5547 Female Old B 0.257
4 5979 Male Old C 0.404
5 5660 Male Old A 0.398
6 5876 Female Old D 0.426
7 5518 Male Old A 0.404
8 6001 Female Old D 0.392
9 6042 Male Old A 0.388
10 5821 Male Old A 0.344
“`

“`ROI“` is a region of interest within each subject, so all subjects have all 4 ROIs.

I would like to calculate a 2-way ANCOVA 4(ROIs [a/b/c/d] – within) x 2 (Age [young/old] – between) + Gender [covariate] to determine the interaction effects of `age` and `ROI` on `value`, controlling for `Gender`.

To do that, I calculated:
“`
#2-way ANOVA
res.aov2 %
anova_test(value ~ Gender + Age*ROI, within = ROI, wid= DTI_ID)
get_anova_table(res.aov2)
“`
which works fine and outputs:
“`
ANOVA Table (type II tests)

Effect DFn DFd F p p<.05 ges
1 Gender 1 1227 5.196 2.30e-02 * 0.004000
2 Age 1 1227 0.732 3.92e-01 0.000596
3 ROI 3 1227 228.933 6.13e-118 * 0.359000
4 Age:ROI 3 1227 22.258 4.90e-14 * 0.052000
“`
I then want to run a multiple comparisons to generate p values that I can graph over boxplots for visualization of the analyses.

I am using `emmeans_test`:
“`
# Pairwise comparisons
pwc2 %
group_by(ROI) %>%
emmeans_test(value ~ Age, covariate = Gender,
p.adjust.method = “bonferroni”)
“`

but receive the error:
“`
Error in contrast.emmGrid(res.emmeans, by = grouping.vars, method = method, : Nonconforming number of contrast coefficients
“`

I cannot figure out why, as the pairwise comparison works fine when I remove the covariate. Does it have to do with a categorical variable being used as a covariate? I am stuck and want to make sure I am reporting the appropriate p-values in my chart.

Reply
Eva

04 May 2021

My final result for one-way ANCOVA is: F(1, 30) = 12.101, p = 0.002
Is this significant?

Reply
Keity Farfan

08 Oct 2021

Hello, thanks for all the information. For example, if my data set does not meet the assumption of normality, and have outilers, which one alternative can I use to analyze the difference between my regression lines?

Reply
Jaden Nyberg

25 Nov 2021

How do you exclude outliers from the original dataframe (which you read in from, for example in my case, a csv file) based on the output from:
“model.metrics %>%
filter(abs(.std.resid) > 3) %>%
as.data.frame()” ?
In essence, I want to just delete a couple of outliers that were detected using this function before calculating the two-way ANCOVA. Thank you.

Reply
ANTHONY

16 Apr 2022

ANCOVA is essentially a combination of linear regression and ANOVA using four predictor variables x1, x2, x3, and x4, and one outcome variable, y and how to control for covariates that might influence the outcome.

Reply
Macs

02 May 2022

I’m working on a 2-Factor ANCOVA, very similar to the example here; one factor has 3 levels, and the other has 2 levels. after creating the pwc (pairwise comparisons objects) any manipulations applied result in:
Error: Input must be a vector, not a `tbl_df/tbl/data.frame/rstatix_test/emmeans_test` object.
I double checked myself by executing the exact example here and still run into the same error when I try to run:
pwc %>% filter(exercise == “high”)

I’ve been able to make the line plot for my data and all that is left is to add my significance indicators.

I know tibbles are supposed to be cranky to prevent problems later on but this is the last step and I just want some nice lil stars on my line plot pls

Reply
Macs

02 May 2022

Unsure what my issue is here, but in following the above example for 2-Factor ANCOVA, I keep encountering the following error:

Error: `x` must be a vector, not a `tbl_df/tbl/data.frame/rstatix_test/emmeans_test` object.

This happens for every manipulation I try to do on the pwc object created with:

pwc %
group_by(exercise) %>%
emmeans_test(
score ~ treatment, covariate = age,
p.adjust.method = “bonferroni”
)

as per the example. When I run the next line:

pwc %>% filter(exercise == “high”) #it returns:
Error: `x` must be a vector, not a `tbl_df/tbl/data.frame/rstatix_test/emmeans_test` object.

Where this is more frustrating is in (trying to) add the significance indicators to the plot, which delivers the same error text. Please help a poor grad student that doesn’t totally understand tibbles.

Reply
MG

25 May 2022

Hi!

What does happen when an assumption is not met?

thank you!

Reply
Rainer

14 Nov 2022

Hello,

The anova_test function uses Type II sum of suares as default. I think this is not optimal for factorial designs with interactions and/or unbalanced designs (which I would assume to be most common).
Therefore, I think if would be more useful to use type III SS, by using “type=3” in the anova_test function or at least to mention this option in the text.

Many thanks for your work,
Rainer

Reply
Andrii

21 Apr 2023

Hello,

You created an amazing site. Thank you!

I see a problem with the computation part. You suggest running age as a covariate in this manner:

res.aov %
anova_test(score ~ age + treatment*exercise)
get_anova_table(res.aov)

However, age, in this case, reports on a separate line as a main effect, not a covariate. Wouldn’t it be correct to quantify an interaction between age and exercise instead?

res.aov %
anova_test(score ~ treatment*exercise + age:exercise)
get_anova_table(res.aov)

In this case, age is not a main effect but rather a covariate to exercise calculated to explain the score.

Keep up the amazing work,
Andrii

Reply