How to Normalize and Standardize Data in R for Great Heatmap Visualization

Prerequisites

The heatmaply R package will be used to interactively visualize the data before and after transformation.

Install the packages using install.packages("heatmaply"), then load it as follow:

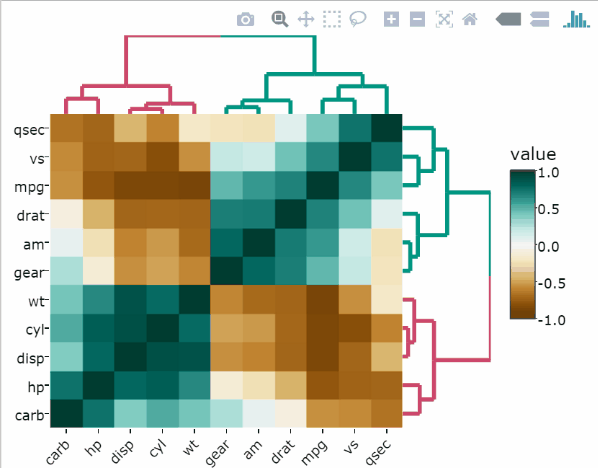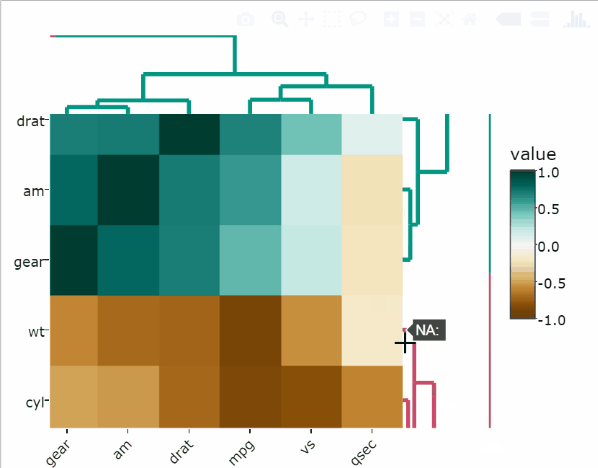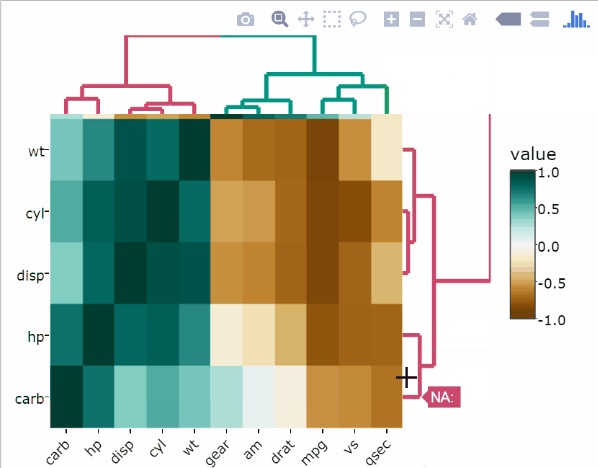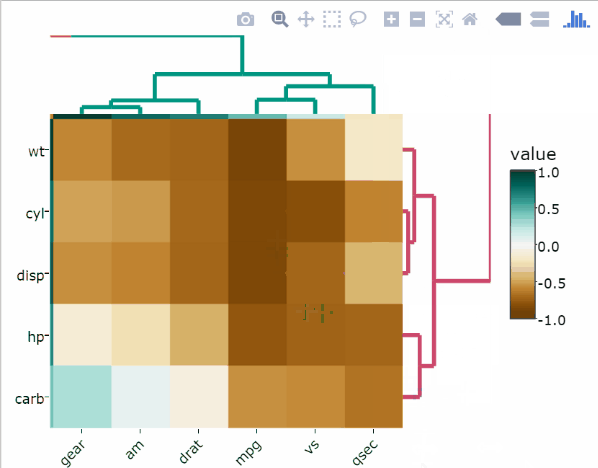
library(heatmaply)

Heatmap of the raw data

heatmaply(
  mtcars, 
  xlab = "Features",
  ylab = "Cars", 
  main = "Raw data"
)

Standard scaling

Standard scaling, also known as standardization or Z-score normalization, consists of subtracting the mean and divide by the standard deviation. In such a case, each value would reflect the distance from the mean in units of standard deviation.

If we would assume all variables come from some normal distribution, then scaling would bring them all close to the standard normal distribution. The resulting distribution has a mean of 0 and a standard deviation of 1.

Standard scaling formula:

\[Transformed.Values = \frac{Values - Mean}{Standard.Deviation}\]

An alternative to standardization is the mean normalization, which resulting distribution will have between -1 and 1 with mean = 0.

Mean normalization formula:

\[Transformed.Values = \frac{Values - Mean}{Maximum - Minimum}\]

The following R code standardizes the mtcars data set and creates a heatmap:

heatmaply(
  scale(mtcars), 
  xlab = "Features",
  ylab = "Cars", 
  main = "Data Scaling"
)

Normalization

When variables in the data comes from possibly different (and non-normal) distributions, other transformations may be in order. Another possibility is to normalize the variables to brings data to the 0 to 1 scale by subtracting the minimum and dividing by the maximum of all observations.

This preserves the shape of each variable’s distribution while making them easily comparable on the same “scale”.

Formula to normalize data between 0 and 1 :

\[Transformed.Values = \frac{Values - Minimum}{Maximum - Minimum}\]

Formula to rescale the data between an arbitrary set of values [a, b]:

\[
Transformed.Values = a + \frac{(Values - Minimum)(b-a)}{Maximum - Minimum}
\]

where a,b are the min-max values.

Normalize data in R. Using the Min-Max normalization function on mtcars data easily reveals columns with only two (am, vs) or three (gear, cyl) variables compared with variables that have a higher resolution of possible values:

heatmaply(
  normalize(mtcars),
  xlab = "Features",
  ylab = "Cars", 
  main = "Data Normalization"
)

Percentile transformation

An alternative to normalize is the percentize function. This is similar to ranking the variables, but instead of keeping the rank values, divide them by the maximal rank. This is done by using the ecdf of the variables on their own values, bringing each value to its empirical percentile. The benefit of the percentize function is that each value has a relatively clear interpretation, it is the percent of observations with that value or below it.

heatmaply(
  percentize(mtcars),
  xlab = "Features",
  ylab = "Cars", 
  main = "Percentile Transformation"
)

References

• Introduction to heatmaply