T-Test Essentials: Definition, Formula and Calculation

Prerequisites

Make sure you have installed the following R packages:

• tidyverse for data manipulation and visualization
• ggpubr for creating easily publication ready plots
• rstatix provides pipe-friendly R functions for easy statistical analyses.
• datarium: contains required data sets for this chapter.

Start by loading the following required packages:

library(tidyverse)
library(ggpubr)
library(rstatix)

Demo data

Here, we’ll use a demo dataset mice2 [datarium package], which contains the weight of 10 mice before and after the treatment.

# Wide format
data("mice2", package = "datarium")
head(mice2, 3)

##   id before after
## 1  1    187   430
## 2  2    194   404
## 3  3    232   406

# Transform into long data: 
# gather the before and after values in the same column
mice2.long <- mice2 %>%
  gather(key = "group", value = "weight", before, after)
head(mice2.long, 3)

##   id  group weight
## 1  1 before    187
## 2  2 before    194
## 3  3 before    232

Summary statistics

Compute some summary statistics (mean and sd) by groups:

mice2.long %>%
  group_by(group) %>%
  get_summary_stats(weight, type = "mean_sd")

## # A tibble: 2 x 5
##   group  variable     n  mean    sd
##   <chr>  <chr>    <dbl> <dbl> <dbl>
## 1 after  weight      10  400.  30.1
## 2 before weight      10  201.  20.0

Calculation

# Save the data in two different vector
before <- mice2$before
after <- mice2$after
# Compute t-test
res <- t.test(before, after, paired = TRUE)
res

## 
##  Paired t-test
## 
## data:  before and after
## t = -30, df = 9, p-value = 1e-09
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -217 -182
## sample estimates:
## mean of the differences 
##                    -199

# Compute t-test
res <- t.test(weight ~ group, data = mice2.long, paired = TRUE)
res

stat.test <- mice2.long  %>% 
  t_test(weight ~ group, paired = TRUE) %>%
  add_significance()
stat.test

## # A tibble: 1 x 9
##   .y.    group1 group2    n1    n2 statistic    df             p p.signif
##   <chr>  <chr>  <chr>  <int> <int>     <dbl> <dbl>         <dbl> <chr>   
## 1 weight after  before    10    10      25.5     9 0.00000000104 ****

mice2.long %>%
  t_test(weight ~ group, paired = TRUE, detailed = TRUE) %>%
  add_significance()

## # A tibble: 1 x 14
##   estimate .y.    group1 group2    n1    n2 statistic             p    df conf.low conf.high method alternative p.signif
##      <dbl> <chr>  <chr>  <chr>  <int> <int>     <dbl>         <dbl> <dbl>    <dbl>     <dbl> <chr>  <chr>       <chr>   
## 1     199. weight after  before    10    10      25.5 0.00000000104     9     182.      217. T-test two.sided   ****

Interpretation

The p-value of the test is 1.0410^{-9}, which is less than the significance level alpha = 0.05. We can then reject null hypothesis and conclude that the average weight of the mice before treatment is significantly different from the average weight after treatment with a p-value = 1.0410^{-9}.

Effect size

The effect size for a paired-samples t-test can be calculated by dividing the mean difference by the standard deviation of the difference, as shown below.

Cohen’s d formula:

\[
d = \frac{mean_D}{SD_D}
\]

Where D is the differences of the paired samples values.

Calculation:

mice2.long  %>% cohens_d(weight ~ group, paired = TRUE)

## # A tibble: 1 x 7
##   .y.    group1 group2 effsize    n1    n2 magnitude
## * <chr>  <chr>  <chr>    <dbl> <int> <int> <ord>    
## 1 weight after  before    8.08    10    10 large

Report

We could report the result as follow: The average weight of mice was significantly increased after treatment, t(9) = 25.5, p < 0.0001, d = 8.07.

Visualize the results:

# Create a box plot
bxp <- ggpaired(mice2.long, x = "group", y = "weight", 
         order = c("before", "after"),
         ylab = "Weight", xlab = "Groups")

# Add p-value and significance levels
stat.test <- stat.test %>% add_xy_position(x = "group")
bxp + 
  stat_pvalue_manual(stat.test, tip.length = 0) +
  labs(subtitle = get_test_label(stat.test, detailed= TRUE))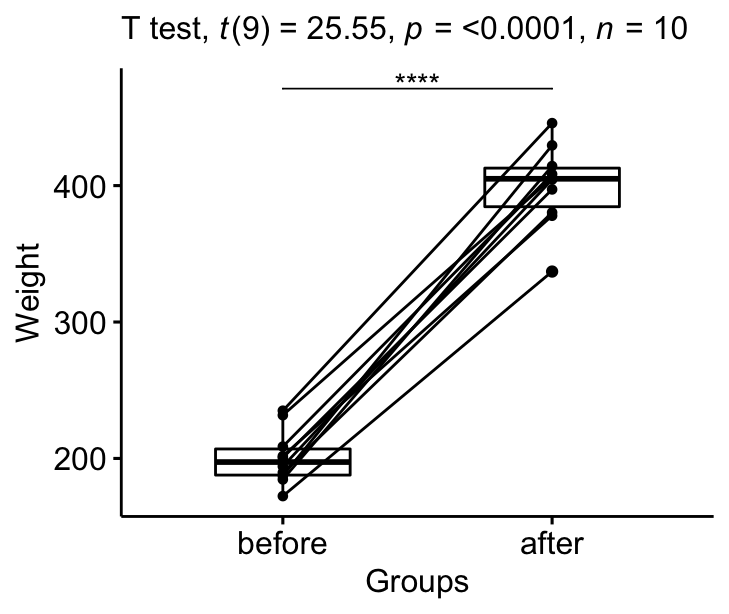

Summary

This article shows how to perform the paired t-test in R/Rstudio using two different ways: the R base function t.test() and the t_test() function in the rstatix package. We also describe how to interpret and report the t-test results.